
【题目】已知点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 右顶点与上顶点,坐标原点
右顶点与上顶点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且点
,且点![]() 是圆
是圆![]() 的圆心,动直线
的圆心,动直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点.
两点.
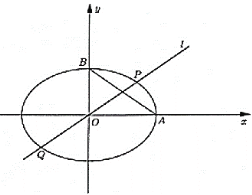
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 在线段
在线段![]() 上,
上,![]() ,且当
,且当![]() 取最小值时直线
取最小值时直线![]() 与圆
与圆![]() 相切,求
相切,求![]() 的值;
的值;
(3)若直线![]() 与圆
与圆![]() 分别交于
分别交于![]() ,
,![]() 两点,点
两点,点![]() 在线段
在线段![]() 上,且
上,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1) 由点![]() 是圆
是圆![]() 的圆心,
的圆心,![]() ,原点
,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,在
,在![]() 中由等面积法有
中由等面积法有 ,可求答案.
,可求答案.
(2) 设![]() ,则
,则![]() ,求出直线
,求出直线![]() 的方程,将点
的方程,将点![]() 坐标代入直线
坐标代入直线![]() 的方程,可得
的方程,可得![]() ,当且仅当
,当且仅当![]()
![]() 时,
时,![]() 取得最小值,可得到点
取得最小值,可得到点![]() 的坐标,则可得到直线
的坐标,则可得到直线![]() 的方程,再由原点
的方程,再由原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,可求出
,可求出![]() 的值.
的值.
(3) 由![]() ,可得
,可得![]() ,求出
,求出![]() ,
,![]() ,可得
,可得 ,可求出
,可求出![]() 的范围.
的范围.
(1)由点![]() 是圆
是圆![]() 的圆心,
的圆心,![]() ,则
,则![]() ,
,![]() ,则
,则![]()
坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,在
,在![]() 中由等面积法有
中由等面积法有 ,可得
,可得![]() .
.
所以椭圆的方程为![]()
(2)设![]() ,则
,则![]()
则![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
将点![]() 坐标代入直线
坐标代入直线![]() 的方程,可得
的方程,可得![]()
故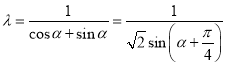 ,则当且仅当
,则当且仅当![]()
![]() 时,
时,![]() 取得最小值.
取得最小值.
此时点![]() 的坐标为
的坐标为 ,直线
,直线![]() 的方程为
的方程为![]() .
.
故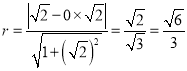 .
.
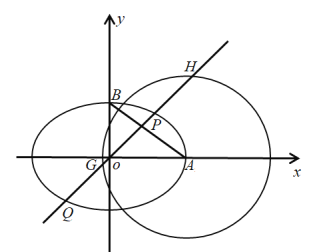
(3)由![]() ,可得
,可得![]() ,将
,将![]() 代入椭圆方程
代入椭圆方程![]() 得:
得:
![]() ,即
,即![]() ,故
,故![]() .
.
又点![]() 到直线
到直线![]() 的距离为
的距离为 ,则
,则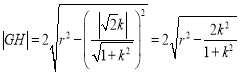
所以![]() ,
,
可得
令![]() ,则
,则![]()
故![]() 取值的范围是
取值的范围是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() ,点P为平面上的动点,过点P作直线l:
,点P为平面上的动点,过点P作直线l:![]() 的垂线,垂足为Q,且
的垂线,垂足为Q,且![]() .
.
![]() Ⅰ
Ⅰ![]() 求动点P的轨迹C的方程;
求动点P的轨迹C的方程;
![]() Ⅱ
Ⅱ![]() 设点P的轨迹C与x轴交于点M,点A,B是轨迹C上异于点M的不同的两点,且满足
设点P的轨迹C与x轴交于点M,点A,B是轨迹C上异于点M的不同的两点,且满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-m|-|2x+2m|(m>0).
(Ⅰ)当m=1时,求不等式f(x)≥1的解集;
(Ⅱ)若x∈R,t∈R,使得f(x)+|t-1|<|t+1|,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村共有100户农民,且都从事蔬菜种植,平均每户的年收入为2万元.为了调整产业结构,该镇政府决定动员部分农民从事蔬菜加工.据估计,若能动员![]() 户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入比上一年提高
户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入比上一年提高![]() ,而从事蔬菜加工的农民平均每户的年收入为
,而从事蔬菜加工的农民平均每户的年收入为![]() 万元.
万元.
(1)在动员![]() 户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前100户农民的总年收入,求
户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前100户农民的总年收入,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,要使这100户农民中从事蔬菜加工的农民的总年收入始终不高于从事蔬菜种植的农民的总年收入,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC﹣A1B1C1的所有棱长都相等,平面BB1C1C⊥平面ABC,BC1=C1C.
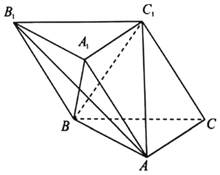
(1)求证:A1B⊥平面AB1C1;
(2)求二面角A1﹣AC1﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长方、堑堵、阳马、鱉臑这些名词出自中国古代数学名著《九章算术商功》.其中阳马和鱉臑是我国古代对一些特殊锥体的称呼.取一长方,如图长方体ABCD﹣A1B1C1D1,按平面ABC1D1斜切一分为二,得到两个一模一样的三棱柱.称该三梭柱为堑堵,再沿堑堵的一顶点与相对的棱剖开,得四棱锥和三棱锥各一个,其中以矩形为底另有一棱与底面垂直的四梭锥D1﹣ABCD称为阳马,余下的三棱锥D1﹣BCC1是由四个直角三角形组成的四面体称为鱉臑.已知长方体ABCD﹣A1B1C1D1中,AB=5,BC=4,AA1=3,按以上操作得到阳马.则该阳马的最长棱长为_____.
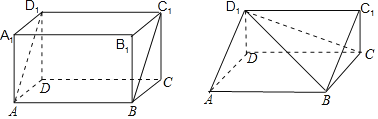
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com