练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

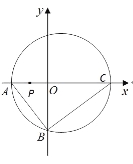
    【题目】如图，直角三角形的顶点坐标，直角顶点，顶点在轴上，点为线段的中点，三角形外接圆的圆心为．

    （1）求边所在直线方程；

    （2）求圆的方程；

    （3）直线过点且倾斜角为，求该直线被圆截得的弦长．

    【答案】（1）（2）（3）

    【解析】

    试题分析：（1）求出BC的斜率，可得BC边所在直线方程；（2）求出圆心与半径，即可求圆M的方程；（3）直线l过点P且倾斜角为，得出直线方程，即可求该直线被圆M截得的弦长

    试题解析：（1）∵ ……1分

    ∴∴ ……4分

    （2）在上式中，令得： ……5分

    ∴圆心 又∵ …… 7分

    ∴外接圆的方程为 ……9分

    （3）∵直线过点且倾斜角为

    直线的方程为 ……10分

    点M到直线的距离为 ……12分

    直线被圆截得的弦长为。 ……14分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知圆外的有一点，过点作直线.

    （1）当直线过圆心时，求直线的方程；

    （2）当直线与圆相切时，求直线的方程；

    （3）当直线的倾斜角为时，求直线被圆所截得的弦长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

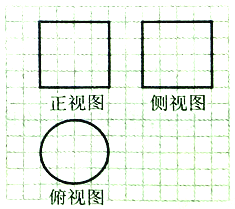
    【题目】《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．如图，网格纸上正方形小格的边长为1，图中粗线画出的是某几何体毛坯的三视图，第一次切削，将该毛坯得到一个表面积最大的长方体；第二次切削沿长方体的对角面刨开，得到两个三棱柱；第三次切削将两个三棱柱分别沿棱和表面的对角线刨开得到两个鳖臑和两个阳马，则阳马与鳖臑的体积之比为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆.

    （1）求证：对任意实数，该圆恒过一定点；

    （2）若该圆与圆外切，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，矩形ABCD的一边AB在x轴上，另一边CD在x轴上方，且AB＝8，BC＝6，其中A（－4，0）、B（4，0）

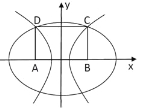
    （1）若A、B为椭圆的焦点，且椭圆经过C、D两点，求该椭圆的方程；

    （2）若A、B为双曲线的焦点，且双曲线经过C、D两点，求双曲线的方程；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，以坐标原点为极点，轴的非负半轴为极轴建立极坐标系．已知点的极坐标为，曲线 的参数方程为（为参数）．

    （1）直线过且与曲线相切，求直线的极坐标方程；

    （2）点与点关于轴对称，求曲线上的点到点的距离的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设不等式组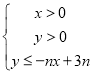所表示的平面区域为Dn，记Dn内的格点（格点即横坐标和纵坐标均为整数的点）的个数为f(n)(n∈N*).

    （1）求f(1)、f(2)的值及f(n)的表达式；

    （2）设bn=2nf(n)，Sn为{bn}的前n项和，求Sn；

    （3）记,若对于一切正整数n，总有Tn≤m成立，求实数m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的中心在原点，焦点在轴上，离心率为，右焦点到右顶点的距离为．

    （1）求椭圆的标准方程；

    （2）是否存在与椭圆交于两点的直线，使得成立？若存在，求出实数的取值范围，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地为制定初中七、八、九年级学生校服的生产计划，有关部门准备对180名初中男生的身高作调查．

    （1）为了达到估计该地初中三个年级男生身高分布的目的，你认为采用怎样的调查方案比较合理？

    （2）表中的数据是使用了某种调查方法获得的：七、八、九年级180名男生身高：

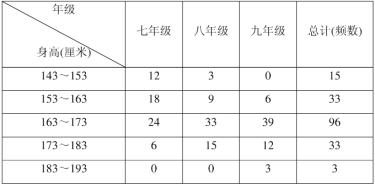
    注：表中每组可含最低值，不含最高值．

    根据表中的数据，请你给校服生产厂家指定一份生产计划思路．

    查看答案和解析>>

    同步练习册答案