
【题目】已知函数![]()
![]() 在
在![]() 上单调递增,
上单调递增,
(1)若函数![]() 有实数零点,求满足条件的实数
有实数零点,求满足条件的实数![]() 的集合
的集合![]() ;
;
(2)若对于任意的![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)数形结合, ![]() 开口向上,对称轴为
开口向上,对称轴为![]() ,与
,与![]() 轴交于点
轴交于点![]() 图象有两种可能,一是对称轴在
图象有两种可能,一是对称轴在![]() 轴左侧,另一个是,对称轴在
轴左侧,另一个是,对称轴在![]() 轴右侧,为使函数
轴右侧,为使函数![]() 有实数零点,则函数图象应与
有实数零点,则函数图象应与![]() 轴有大于零的交点横坐标,所以,对称轴应在
轴有大于零的交点横坐标,所以,对称轴应在![]() 轴右侧,即
轴右侧,即![]() ,又因为
,又因为![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ;
;
(2)令![]() ,只需
,只需![]() 且
且![]() 解不等式组,即可求
解不等式组,即可求![]() 的取值范围.
的取值范围.
试题解析: (1)函数![]() 级
级![]() 单调递增区间是
单调递增区间是![]() ,因为
,因为![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ;
;
令![]()
![]() ,则
,则![]()
![]()
函数![]() 有实数零点,即:
有实数零点,即: ![]() 在
在![]() 上有零点,只需:
上有零点,只需:
方法一 解得
解得![]()
方法二![]() 解得
解得![]()
综上: ![]() ,即
,即![]()
(2)![]() 化简得
化简得![]()
因为对于任意的![]() 时,不等式
时,不等式![]() 恒成立,
恒成立,
即对于![]() 不等式
不等式![]() 恒成立,
恒成立,
设![]() (
(![]() )
)
法一
当![]() 时,即
时,即![]() 不符合题意
不符合题意
当![]() 时,即
时,即![]() ,只需
,只需![]()
得![]() 从而
从而![]()
当![]() ,即
,即![]() ,只需
,只需![]()
得![]() 或
或![]() ,与
,与![]() 矛盾
矛盾
法二 得
得![]()
综上知满足条件的![]() 的范围为
的范围为![]()


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人练习罚球,每人练习6组,每组罚球20个,命中个数的茎叶图如下:
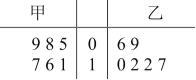
(1)求甲命中个数的中位数和乙命中个数的众数;
(2)通过计算,比较甲乙两人的罚球水平.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第![]() 届夏季奥林匹克运动会2016年8月5日到2016年8月21日在巴西里约热内卢举行,为了解我校学生“收看奥运会足球赛”是否与性別有关,从全校学生中随机抽取
届夏季奥林匹克运动会2016年8月5日到2016年8月21日在巴西里约热内卢举行,为了解我校学生“收看奥运会足球赛”是否与性別有关,从全校学生中随机抽取![]() 名进行了问卷调查,得到
名进行了问卷调查,得到![]() 列联表,从这
列联表,从这![]() 名同学中随机抽取
名同学中随机抽取![]() 人,抽到“收看奥运会足球赛 ”的学生的概率是
人,抽到“收看奥运会足球赛 ”的学生的概率是![]() .
.
男生 | 女生 | 合计 | |
收看 |
| ||
不收看 |
| ||
合计 |
|
(1)请将上面的![]() 列联表补充完整,并据此资料分析“收看奥运会足球赛”与性別是否有关;
列联表补充完整,并据此资料分析“收看奥运会足球赛”与性別是否有关;
(2)若从这![]() 名同学中的男同学中随机抽取
名同学中的男同学中随机抽取![]() 人参加有奖竞猜活动,记抽到收看奥运会足球赛”的学生人数为
人参加有奖竞猜活动,记抽到收看奥运会足球赛”的学生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:
 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)在(1)的条件下,若![]() 是函数
是函数![]() 的零点,且
的零点,且![]() ,求
,求![]() 的值;
的值;
(3)当![]() 时,函数
时,函数![]() 有两个零点
有两个零点![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若某产品的直径长与标准值的差的绝对值不超过1mm时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位:mm),将所得数据分组,得到如下频率分布表:
分 组 | 频 数 | 频 率 |
[-3,-2) | 0.10 | |
[-2,-1) | 8 | |
(1,2] | 0.50 | |
(2,3] | 10 | |
(3,4] | ||
合计 | 50 | 1.00 |
(1)将上面表格中缺少的数据填充完整.
(2)估计该厂生产的此种产品中,不合格品的直径长与标准值的差落在区间(1,3]内的概率.
(3)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品.据此估算这批产品中的合格品的件数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com