
函数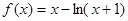 ,数列
,数列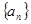 ,满足0<
,满足0<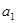 <1,
<1,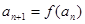 ,数列
,数列 满足
满足 ,
,
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)求证:0< <
< <1;
<1;
(Ⅲ)若 且
且 <
< ,则当n≥2时,求证:
,则当n≥2时,求证: >
>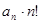
(Ⅰ)函数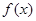 的递减区间(-1,0),递增区间(0,+
的递减区间(-1,0),递增区间(0,+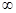 );(Ⅱ)详见解析;(Ⅲ)详见解析.
);(Ⅱ)详见解析;(Ⅲ)详见解析.
【解析】
试题分析:(Ⅰ)求函数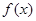 的单调区间,首先确定定义域
的单调区间,首先确定定义域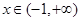 ,可通过单调性的定义,或求导确定单调区间,由于
,可通过单调性的定义,或求导确定单调区间,由于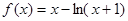 ,含有对数函数,可通过求导来确定单调区间,对函数
,含有对数函数,可通过求导来确定单调区间,对函数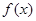 求导得
求导得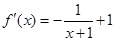 ,由此令
,由此令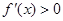 ,
, ,解出
,解出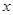 就能求出函数
就能求出函数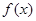 的单调区间;(Ⅱ)求证:0<
的单调区间;(Ⅱ)求证:0<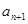 <
< <1,可先证0<
<1,可先证0< <1,
<1,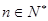 ,再证数列
,再证数列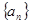 单调递减,可先证0<
单调递减,可先证0< <1,若能求出通项公式,利用通项公式来证,由已知0<
<1,若能求出通项公式,利用通项公式来证,由已知0<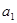 <1,
<1,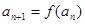 ,显然无法求通项公式,可考虑利用数学归纳法来证,结合函数
,显然无法求通项公式,可考虑利用数学归纳法来证,结合函数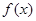 的单调性易证,证数列
的单调性易证,证数列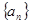 单调递减,可用作差比较法
单调递减,可用作差比较法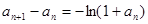 <0证得,从而的结论;(Ⅲ)若
<0证得,从而的结论;(Ⅲ)若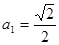 且
且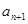 <
<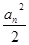 ,则当n≥2时,求证:
,则当n≥2时,求证: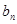 >
> ,关键是求
,关键是求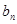 的通项公式,由
的通项公式,由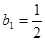 ,
,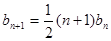 ,所以
,所以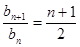 ,可得
,可得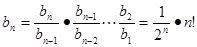 ,只要证明
,只要证明 >
> ,,即证
,,即证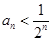 ,因为
,因为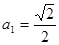 且
且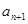 <
<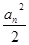 ,则
,则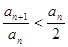 ,由此可得
,由此可得 ,所以
,所以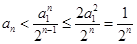 ,即证得.
,即证得.
试题解析:(Ⅰ)利用导数可求得函数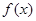 的递减区间(-1,0),递增区间(0,+
的递减区间(-1,0),递增区间(0,+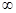 )
)
(Ⅱ)先用数学归纳法证明0< <1,
<1,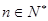 .
.
①当n=1时,由已知得结论成立.②假设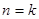 时,0<
时,0<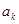 <1成立.则当
<1成立.则当 时由(1)可得函数
时由(1)可得函数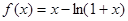 在
在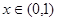 上是增函数,所以
上是增函数,所以
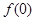 <
<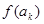 <
<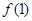 =1-
=1-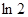 <1,所以0<
<1,所以0<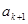 <1,即n=k+1时命题成立,由①②可得0<
<1,即n=k+1时命题成立,由①②可得0< <1,
<1,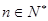 成立.
成立.
又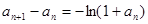 <0,所以
<0,所以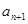 <
< 成立.
成立.
所以0<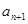 <
< <1
<1
(Ⅲ)因为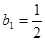 ,
,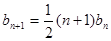 ,所以
,所以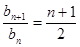 ,
,
所以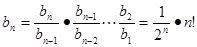 ……①
……①
因为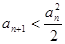 则
则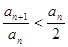 ,所以
,所以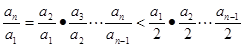
因为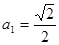 ,当
,当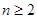 时,
时,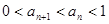 ,
,
所以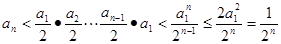 ……②
……②
由①②两式可知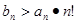
考点:函数与导数,函数单调性,数学归纳法,叠乘法求数列的通项公式,放缩法.


 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
| a1-b | a1lnb |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| 2n |
| 1 |
| f′(an) |
| (2n-1)(2an-1) |
| an |
| lim |
| n→∞ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| 1 |
| 2n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com