
【题目】设函数f(x)=sin(ωx﹣ ![]() )+sin(ωx﹣
)+sin(ωx﹣ ![]() ),其中0<ω<3,已知f(
),其中0<ω<3,已知f( ![]() )=0.(12分)
)=0.(12分)
(Ⅰ)求ω;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移 ![]() 个单位,得到函数y=g(x)的图象,求g(x)在[﹣
个单位,得到函数y=g(x)的图象,求g(x)在[﹣ ![]() ,
, ![]() ]上的最小值.
]上的最小值.
【答案】解:(Ⅰ)函数f(x)=sin(ωx﹣ ![]() )+sin(ωx﹣
)+sin(ωx﹣ ![]() )
)
=sinωxcos ![]() ﹣cosωxsin
﹣cosωxsin ![]() ﹣sin(
﹣sin( ![]() ﹣ωx)
﹣ωx)
= ![]() sinωx﹣
sinωx﹣ ![]() cosωx
cosωx
= ![]() sin(ωx﹣
sin(ωx﹣ ![]() ),
),
又f( ![]() )=
)= ![]() sin(
sin( ![]() ω﹣
ω﹣ ![]() )=0,
)=0,
∴ ![]() ω﹣
ω﹣ ![]() =kπ,k∈Z,
=kπ,k∈Z,
解得ω=6k+2,
又0<ω<3,
∴ω=2;
(Ⅱ)由(Ⅰ)知,f(x)= ![]() sin(2x﹣
sin(2x﹣ ![]() ),
),
将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得到函数y= ![]() sin(x﹣
sin(x﹣ ![]() )的图象;
)的图象;
再将得到的图象向左平移 ![]() 个单位,得到y=
个单位,得到y= ![]() sin(x+
sin(x+ ![]() ﹣
﹣ ![]() )的图象,
)的图象,
∴函数y=g(x)= ![]() sin(x﹣
sin(x﹣ ![]() );
);
当x∈[﹣ ![]() ,
, ![]() ]时,x﹣
]时,x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
∴sin(x﹣ ![]() )∈[﹣
)∈[﹣ ![]() ,1],
,1],
∴当x=﹣ ![]() 时,g(x)取得最小值是﹣
时,g(x)取得最小值是﹣ ![]() ×
× ![]() =﹣
=﹣ ![]() .
.
【解析】(Ⅰ)利用三角恒等变换化函数f(x)为正弦型函数,根据f( ![]() )=0求出ω的值;
)=0求出ω的值;
(Ⅱ)写出f(x)解析式,利用平移法则写出g(x)的解析式,求出x∈[﹣ ![]() ,
, ![]() ]时g(x)的最小值.
]时g(x)的最小值.
【考点精析】解答此题的关键在于理解两角和与差的正弦公式的相关知识,掌握两角和与差的正弦公式:![]() ,以及对函数y=Asin(ωx+φ)的图象变换的理解,了解图象上所有点向左(右)平移
,以及对函数y=Asin(ωx+φ)的图象变换的理解,了解图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:高中数学 来源: 题型:
【题目】为了实现绿色发展,避免浪费能源,某市政府计划对居民用电采用阶梯收费的方法.为此,相关部分在该市随机调查了![]() 户居民六月份的用电量(单位:
户居民六月份的用电量(单位:![]() )和家庭收入(单位:万元),以了解这个城市家庭用电量的情况.
)和家庭收入(单位:万元),以了解这个城市家庭用电量的情况.
用电量数据如下:
![]() .
.
对应的家庭收入数据如下:
![]()
![]() .
.
(Ⅰ)根据国家发改委的指示精神,该市计划实施![]() 阶阶梯电价,使
阶阶梯电价,使![]() 的用户在第一档,电价为
的用户在第一档,电价为![]() 元/
元/![]() ;
;![]() 的用户在第二档,电价为
的用户在第二档,电价为![]() 元/
元/![]() ;
;![]() 的用户在第三档,电价为
的用户在第三档,电价为![]() 元/
元/![]() ,试求出居民用电费用
,试求出居民用电费用![]() 与用电量
与用电量![]() 间的函数关系;
间的函数关系;
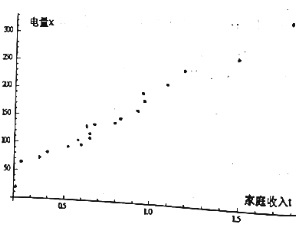
(Ⅱ)以家庭收入![]() 为横坐标,电量
为横坐标,电量![]() 为纵坐标作出散点图(如图),求
为纵坐标作出散点图(如图),求![]() 关于
关于![]() 的回归直线方程(回归直线方程的系数四舍五入保留整数).
的回归直线方程(回归直线方程的系数四舍五入保留整数).
(Ⅲ)小明家的月收入![]() 元,按上述关系,估计小明家月支出电费多少元?
元,按上述关系,估计小明家月支出电费多少元?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:一组相关数据![]() ,
,![]() ,…,
,…,![]() 的回归直线方程
的回归直线方程![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为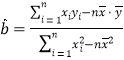 ,
,![]() ,其中
,其中![]() ,
,![]() 为样本均值.
为样本均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=cos(x+ ![]() ),则下列结论错误的是( )
),则下列结论错误的是( )
A.f(x)的一个周期为﹣2π
B.y=f(x)的图象关于直线x= ![]() 对称
对称
C.f(x+π)的一个零点为x= ![]()
D.f(x)在( ![]() ,π)单调递减
,π)单调递减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() ,
,![]() .
.
(1)直线![]() 是否过定点?若过定点,求出该定点坐标,若不过定点,请说明理由;
是否过定点?若过定点,求出该定点坐标,若不过定点,请说明理由;
(2)已知点![]() ,若直线
,若直线![]() 上存在点
上存在点![]() 满足条件
满足条件![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10 ![]() cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(Ⅰ)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(Ⅱ)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.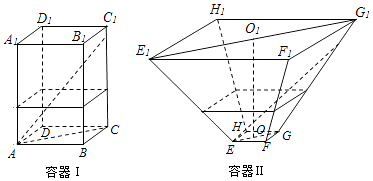
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名同学参加一项射击比赛游戏,其中任何一人每射击一次击中目标得2分,未击中目标得0分.若甲、乙两人射击的命中率分别为 ![]() 和P,且甲、乙两人各射击一次得分之和为2的概率为
和P,且甲、乙两人各射击一次得分之和为2的概率为 ![]() .假设甲、乙两人射击互不影响,则P值为( )
.假设甲、乙两人射击互不影响,则P值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com