
°æƒø°øƒ≥—ß–£π≤”–ΩÃ÷∞π§900»À£¨∑÷≥…»˝∏ˆ≈˙¥ŒΩ¯––ºÃ–¯ΩÔ˝≈‡—µ£¨‘⁄»˝∏ˆ≈˙¥Œ÷–ƒ–°¢≈ÆΩÃ÷∞π§»À ˝»Áœ¬±ÌÀ˘ æ.“—÷™‘⁄»´ÃÂΩÃ÷∞π§÷–Àʪ˙≥È»°“ª√˚£¨≥ÈµΩµ⁄∂˛≈˙¥Œ÷–≈Æ÷∞𧵃∏≈¬ «0.16.
µ⁄“ª≈˙¥Œ | µ⁄∂˛≈˙¥Œ | µ⁄»˝≈˙¥Œ | |
≈ÆΩÃ÷∞π§ | 196 |
|
|
ƒ–ΩÃ÷∞π§ | 204 | 156 |
|
£®1£©«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©œ÷”√∑÷≤„≥È—˘µƒ∑Ω∑®‘⁄»´ÃÂΩÃ÷∞π§÷–≥È»°54√˚◊ˆ≈‡—µ–ßπ˚µƒµ˜≤È£¨Œ ”¶‘⁄µ⁄»˝≈˙¥Œ÷–≥È»°ΩÃ÷∞π§∂‡…Ÿ√˚£ø
£®3£©“—÷™![]() £¨
£¨![]() £¨«Ûµ⁄»˝≈˙¥Œ÷–≈ÆΩÃ÷∞𧱻ƒ–ΩÃ÷∞π§∂‡µƒ∏≈¬ .
£¨«Ûµ⁄»˝≈˙¥Œ÷–≈ÆΩÃ÷∞𧱻ƒ–ΩÃ÷∞π§∂‡µƒ∏≈¬ .
°æ¥∞∏°ø£®1£©![]() £®2£©”¶‘⁄µ⁄»˝≈˙¥Œ÷–≥È»°12√˚£®3£©
£®2£©”¶‘⁄µ⁄»˝≈˙¥Œ÷–≥È»°12√˚£®3£©![]()
°æΩ‚Œˆ°ø
£®1£©‘⁄»´ÃÂΩÃ÷∞π§÷–Àʪ˙≥È»°1√˚£¨≥ÈµΩµ⁄2≈˙¥Œ÷–≈ÆΩà ¶÷∞𧵃∏≈¬ «0.16£¨”√![]() ≥˝“‘◊‹Ã ˝µ»”⁄0.16£¨º¥ø…«Û≥ˆ
≥˝“‘◊‹Ã ˝µ»”⁄0.16£¨º¥ø…«Û≥ˆ![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©∏˘æ›◊‹Ã ˝∫Õµ⁄1≈˙¥Œ∫Õµ⁄2≈˙¥Œµƒ◊‹»À ˝∫Õ◊‹Ã ˝£¨µ√µΩµ⁄»˝≈˙¥Œµƒ»À ˝£¨∏˘æ›√ø∏ˆ∏ˆÃ±ª≥ÈµΩµƒ∏≈¬ £¨¡–≥ˆµ» Ω£¨Ω‚∑Ω≥ú¥ø…£ª
£®3£© ‘—È∑¢…˙∞¸∫¨µƒ ¬º˛ ˝ø…“‘Õ®π˝¡–æŸµ√µΩΩ·π˚£¨¬˙◊„Ãıº˛µƒ ¬º˛“≤ø…“‘Õ®π˝¡–æŸµ√µΩ ¬º˛ ˝£¨‘Ÿ¿˚”√π≈µ‰∏≈–Õµƒ«Û∏≈¬ π´ Ω£¨º∆À„∏≈¬ .
£®1£©”…![]() £¨Ω‚µ√
£¨Ω‚µ√![]() .
.
£®2£©µ⁄»˝≈˙¥Œµƒ»À ˝Œ™![]() £¨
£¨
…Ë”¶‘⁄µ⁄»˝≈˙¥Œ÷–≥È»°![]() √˚£¨‘Ú
√˚£¨‘Ú![]() £¨Ω‚µ√
£¨Ω‚µ√![]() .
.
°‡”¶‘⁄µ⁄»˝≈˙¥Œ÷–≥È»°12√˚.
£®3£©…˵⁄»˝≈˙¥Œ÷–≈ÆΩÃ÷∞𧱻ƒ–ΩÃ÷∞π§∂‡µƒ ¬º˛Œ™![]() £¨µ⁄»˝≈˙¥Œ≈ÆΩÃ÷∞π§∫Õƒ–ΩÃ÷∞π§ ˝º«Œ™ ˝∂‘
£¨µ⁄»˝≈˙¥Œ≈ÆΩÃ÷∞π§∫Õƒ–ΩÃ÷∞π§ ˝º«Œ™ ˝∂‘![]() £¨”…£®2£©÷™£¨
£¨”…£®2£©÷™£¨![]() £®
£®![]() £¨
£¨![]() £¨
£¨![]() £©‘Úª˘±æ ¬º˛◊‹ ˝”–£∫
£©‘Úª˘±æ ¬º˛◊‹ ˝”–£∫
![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨π≤9∏ˆ£¨
£¨π≤9∏ˆ£¨
∂¯ ¬º˛![]() ∞¸∫¨µƒª˘±æ ¬º˛”–£∫
∞¸∫¨µƒª˘±æ ¬º˛”–£∫![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨π≤4∏ˆ£¨
£¨π≤4∏ˆ£¨
°‡![]() .
.



| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() £¨«“∫Ø ˝
£¨«“∫Ø ˝![]() Œ™≈º∫Ø ˝°£
Œ™≈º∫Ø ˝°£
£®1£©«Û![]() µƒΩ‚Œˆ Ω£ª
µƒΩ‚Œˆ Ω£ª
£®2£©»Ù∑Ω≥Ã![]() ”–»˝∏ˆ≤ªÕ¨µƒ µ ˝∏˘£¨«Û µ ˝mµƒ»°÷µ∑∂Œß°£
”–»˝∏ˆ≤ªÕ¨µƒ µ ˝∏˘£¨«Û µ ˝mµƒ»°÷µ∑∂Œß°£
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄Àƒ¿‚◊∂O©ÅABCD÷–£¨µ◊√ÊABCDÀƒ±fl≥§Œ™1µƒ¡‚–Œ£¨°œABC=![]() £¨OA°Õµ◊√ÊABCD£¨OA=2£¨MŒ™OAµƒ÷–µ„£¨NŒ™BCµƒ÷–µ„£Æ
£¨OA°Õµ◊√ÊABCD£¨OA=2£¨MŒ™OAµƒ÷–µ„£¨NŒ™BCµƒ÷–µ„£Æ
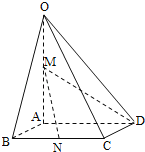
£®1£©÷§√˜£∫÷±œflMN°Œ∆Ω√ÊOCD£ª
£®2£©«Û“Ï√Ê÷±œflAB”ÎMDÀ˘≥…Ω«µƒ¥Û–°£ª
£®3£©«Ûµ„BµΩ∆Ω√ÊOCDµƒæ‡¿Î£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë![]() £¨
£¨![]() «
«![]() µƒ¡Ω∏ˆ∑«ø’◊”ºØ£¨»Áπ˚¥Ê‘⁄“ª∏ˆ∫Ø ˝
µƒ¡Ω∏ˆ∑«ø’◊”ºØ£¨»Áπ˚¥Ê‘⁄“ª∏ˆ∫Ø ˝![]() ¬˙◊„£∫¢Ÿ
¬˙◊„£∫¢Ÿ ![]() £ª¢⁄ ∂‘»Œ“‚
£ª¢⁄ ∂‘»Œ“‚![]() £¨µ±
£¨µ±![]() ±£¨∫„”–
±£¨∫„”–![]() £¨ƒ«√¥≥∆’‚¡Ω∏ˆºØ∫œŒ™°∞
£¨ƒ«√¥≥∆’‚¡Ω∏ˆºØ∫œŒ™°∞![]() µΩ
µΩ![]() µƒ±£–ÚÕ¨ππ°±£¨“‘œ¬ºØ∫œ∂‘≤ª «°∞
µƒ±£–ÚÕ¨ππ°±£¨“‘œ¬ºØ∫œ∂‘≤ª «°∞![]() µΩ
µΩ![]() µƒ±£–ÚÕ¨ππ°±µƒ «£® £©
µƒ±£–ÚÕ¨ππ°±µƒ «£® £©
A.![]() B.
B.![]() £¨
£¨![]()
C.![]() £¨
£¨![]() D.
D.![]() £¨
£¨![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∆Ω√Ê÷±Ω«◊¯±Íœµ![]() £¨÷±œfl
£¨÷±œfl![]() π˝µ„
π˝µ„![]() £¨«“«„–±Ω«Œ™
£¨«“«„–±Ω«Œ™![]() £¨“‘
£¨“‘![]() Œ™º´µ„£¨
Œ™º´µ„£¨![]() ÷·µƒ∑«∏∫∞Î÷·Œ™º´÷·Ω®¡¢º´◊¯±Íœµ£¨‘≤
÷·µƒ∑«∏∫∞Î÷·Œ™º´÷·Ω®¡¢º´◊¯±Íœµ£¨‘≤![]() µƒº´◊¯±Í∑Ω≥ÃŒ™
µƒº´◊¯±Í∑Ω≥ÃŒ™![]() .
.
£®1£©«Û÷±œfl![]() µƒ≤Œ ˝∑Ω≥Ã∫Õ‘≤
µƒ≤Œ ˝∑Ω≥Ã∫Õ‘≤![]() µƒ±Í◊º∑Ω≥ãª
µƒ±Í◊º∑Ω≥ãª
£®2£©…Ë÷±œfl![]() ”Α≤
”Α≤![]() Ωª”⁄
Ωª”⁄![]() °¢
°¢![]() ¡Ωµ„£¨»Ù
¡Ωµ„£¨»Ù![]() £¨«Û÷±œfl
£¨«Û÷±œfl![]() µƒ«„–±Ω«µƒ
µƒ«„–±Ω«µƒ![]() ÷µ.
÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë√¸Ã‚p£∫ µ ˝![]() ¬˙◊„≤ªµ» Ω
¬˙◊„≤ªµ» Ω![]() £ª
£ª
√¸Ã‚q£∫πÿ”⁄![]() ≤ªµ» Ω
≤ªµ» Ω![]() ∂‘»Œ“‚µƒ
∂‘»Œ“‚µƒ![]() ∫„≥…¡¢£Æ
∫„≥…¡¢£Æ
£®1£©»Ù√¸Ã‚![]() Œ™’Ê√¸Ã‚£¨«Û µ ˝
Œ™’Ê√¸Ã‚£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß£ª
µƒ»°÷µ∑∂Œß£ª
£®2£©»Ù°∞![]() °±Œ™ºŸ√¸Ã‚£¨°∞
°±Œ™ºŸ√¸Ã‚£¨°∞![]() °±Œ™’Ê√¸Ã‚£¨«Û µ ˝
°±Œ™’Ê√¸Ã‚£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß.
µƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
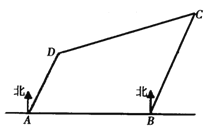
°æƒø°ø»ÁÕº£¨”–Àƒ◊˘≥« –![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() £¨∆‰÷–
£¨∆‰÷–![]() ‘⁄
‘⁄![]() µƒ’˝∂´∑ΩœÚ£¨«“”Î
µƒ’˝∂´∑ΩœÚ£¨«“”Î![]() œ‡æ‡
œ‡æ‡![]() £¨
£¨![]() ‘⁄
‘⁄![]() µƒ±±∆´∂´
µƒ±±∆´∂´![]() ∑ΩœÚ£¨«“”Î
∑ΩœÚ£¨«“”Î![]() œ‡æ‡
œ‡æ‡![]() £ª
£ª![]() ‘⁄
‘⁄![]() µƒ±±∆´∂´
µƒ±±∆´∂´![]() ∑ΩœÚ£¨«“”Î
∑ΩœÚ£¨«“”Î![]() œ‡æ‡
œ‡æ‡![]() £¨“ªº‹∑…ª˙¥”≥« –
£¨“ªº‹∑…ª˙¥”≥« –![]() ≥ˆ∑¢“‘
≥ˆ∑¢“‘![]() µƒÀŸ∂»œÚ≥« –
µƒÀŸ∂»œÚ≥« –![]() ∑…––£¨∑…––¡À
∑…––£¨∑…––¡À![]() £¨Ω”µΩ√¸¡Ó∏ƒ±‰∫ΩœÚ£¨∑…œÚ≥« –
£¨Ω”µΩ√¸¡Ó∏ƒ±‰∫ΩœÚ£¨∑…œÚ≥« –![]() £¨¥À ±∑…ª˙懿Î≥« –
£¨¥À ±∑…ª˙懿Î≥« –![]() ”–£® £©
”–£® £©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥‘À∂Ø÷∆“¬∆∑≈∆Œ™¡À≥…“¬≥fl¥Á∏¸æ´◊º£¨œ÷—°‘Ò15√˚÷æ‘∏’fl£¨∂‘∆‰…Ì∏fl∫Õ±€’πΩ¯––≤‚¡ø£®µ•Œª£∫¿Â√◊£©£¨◊ÛÕºŒ™—°»°µƒ15√˚÷æ‘∏’fl…Ì∏fl”α€’𵃒€œflÕº£¨”“ÕºŒ™…Ì∏fl”α€’πÀ˘∂‘”¶µƒ…¢µ„Õº£¨≤¢«Ûµ√∆‰ªÿπÈ∑Ω≥ÃŒ™![]() £¨“‘œ¬Ω·¬€÷–≤ª’˝»∑µƒŒ™
£¨“‘œ¬Ω·¬€÷–≤ª’˝»∑µƒŒ™


A. 15√˚÷æ‘∏’fl…Ì∏flµƒº´≤Ó–°”⁄±€’πµƒº´≤Ó
B. 15√˚÷æ‘∏’fl…Ì∏fl∫Õ±€’π≥…’˝œ‡πÿπÿœµ£¨
C. ø…π¿º∆…Ì∏flŒ™190¿Â√◊µƒ»À±€’π¥Û‘ºŒ™189.65¿Â√◊£¨
D. …Ì∏flœ‡≤Ó10¿Â√◊µƒ¡Ω»À±€’π∂ºœ‡≤Ó11.6¿Â√◊£¨
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øæ≠º√∂©ªı≈˙¡øƒ£–Õ£¨ «ƒø«∞¥Û∂‡ ˝π§≥ß°¢∆Û“µµ»◊Ó≥£≤…”√µƒ∂©ªı∑Ω Ω£¨º¥ƒ≥÷÷ŒÔ◊ ‘⁄µ•Œª ±º‰µƒ–Ë«Û¡øŒ™ƒ≥≥£ ˝£¨æ≠π˝ƒ≥∂Œ ±º‰∫Û£¨¥Ê¥¢¡øœ˚∫ƒœ¬ΩµµΩ¡„£¨¥À ±ø™ º∂©ªı≤¢Àʺ¥µΩªı£¨»ª∫Ûø™ ºœ¬“ª∏ˆ¥Ê¥¢÷‹∆⁄£¨∏√ƒ£–Õ ”√”⁄’˚≈˙º‰∏ÙΩ¯ªı°¢≤ª‘ –Ì»±ªıµƒ¥Ê¥¢Œ £¨æflûÁœ¬£∫ƒÍ¥Ê¥¢≥…±æ∑—![]() £®‘™£©πÿ”⁄√ø¥Œ∂©ªı
£®‘™£©πÿ”⁄√ø¥Œ∂©ªı![]() £®µ•Œª£©µƒ∫Ø ˝πÿœµ
£®µ•Œª£©µƒ∫Ø ˝πÿœµ![]() £¨∆‰÷–
£¨∆‰÷–![]() Œ™ƒÍ–Ë«Û¡ø£¨
Œ™ƒÍ–Ë«Û¡ø£¨![]() Œ™√øµ•ŒªŒÔ◊ µƒƒÍ¥Ê¥¢∑—£¨
Œ™√øµ•ŒªŒÔ◊ µƒƒÍ¥Ê¥¢∑—£¨![]() Œ™√ø¥Œ∂©ªı∑—. ƒ≥ªØπ§≥ß–Ë”√º◊¥º◊˜Œ™‘≠¡œ£¨ƒÍ–Ë«Û¡øŒ™6000∂÷£¨√ø∂÷¥Ê¥¢∑—Œ™120‘™/ƒÍ£¨√ø¥Œ∂©ªı∑—Œ™2500‘™.
Œ™√ø¥Œ∂©ªı∑—. ƒ≥ªØπ§≥ß–Ë”√º◊¥º◊˜Œ™‘≠¡œ£¨ƒÍ–Ë«Û¡øŒ™6000∂÷£¨√ø∂÷¥Ê¥¢∑—Œ™120‘™/ƒÍ£¨√ø¥Œ∂©ªı∑—Œ™2500‘™.
£®1£©»Ù∏√ªØπ§≥ß√ø¥Œ∂©π∫300∂÷º◊¥º£¨«ÛƒÍ¥Ê¥¢≥…±æ∑—£ª
£®2£©√ø¥Œ–Ë∂©π∫∂‡…Ÿ∂÷º◊¥º£¨ø… π∏√ªØπ§≥߃ͥʥ¢≥…±æ∑—◊Ó…Ÿ£ø◊Ó…Ÿ∑—”√Œ™∂‡…Ÿ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com