练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (本题满分15分) 已知函数f(x)＝x3＋ax2＋bx，a , bR．
    (Ⅰ) 曲线C：y＝f(x) 经过点P(1，2)，且曲线C在点P处的切线平行于直线y＝2x＋1，求a，b的值；
    (Ⅱ) 已知f(x)在区间(1，2) 内存在两个极值点，求证：0＜a＋b＜2

    (Ⅰ)解: ＝，
    由题设知： 解得     
    (Ⅱ)解：因为在区间内存在两个极值点，
    所以，即在内有两个不等的实根．
    故
    由(1)+(3)得.
    由（4）得，
    因，故，从而.
    所以．                       

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    时下，网校教学越来越受到广大学生的喜爱，它已经成为学生们课外学习的一种趋势，假设某网校的套题每日的销售量（单位：千套）与销售价格（单位：元/套）满足的关系式，其中，为常数.已知销售价格为4元/套时，每日可售出套题21千套.
    （1）求的值；
    （2）假设网校的员工工资，办公等所有开销折合为每套题2元（只考虑销售出的套数），试确定销售价格的值，使网校每日销售套题所获得的利润最大.（保留1位小数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设，其中
    （Ⅰ）当时，求的极值点；
    （Ⅱ）若为R上的单调函数，求a的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f(x)＝2x－－aln(x＋1)，a∈R．
    （1）若a＝－4，求函数f(x)的单调区间；
    （2）求y＝f(x)的极值点（即函数取到极值时点的横坐标）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数 
    （1）若函数的图象在处的切线方程为，求的值；
    （2）若函数在上是增函数，求的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分13分）
    已知函数,，其中R．
    （1）当a=1时，判断的单调性；
    （2）若在其定义域内为增函数，求正实数的取值范围；
    （3）设函数,当时，若，，总有
    成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分分）
    已知函数.当时，函数取得极值.
    （I）求实数的值；
    （II）若时，方程有两个根，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题


    （1）当时，在上恒成立，求实数的取值范围；
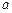    （2）当时，若函数在上恰有两个不同零点，求实数的取值范围；
    （3）是否存在实数，使函数f（x）和函数在公共定义域上具有相同的单调区间？若存在，求出的值，若不存在，说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数
    （1）求函数的极大值； （2）
    （3）对于函数定义域上的任意实数，若存在常数，使得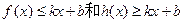都成立，则称直线为函数的分界线。设，试探究函数是否存在“分界线”？若存在，请给予证明，并求出的值；若不存在，请说明理由

    查看答案和解析>>

    同步练习册答案