
【题目】选修4﹣4:坐标系与参数方程
在平面直角坐标系x0y中,动点A的坐标为(2﹣3sinα,3cosα﹣2),其中α∈R.在极坐标系(以原点O为极点,以x轴非负半轴为极轴)中,直线C的方程为ρcos(θ﹣ ![]() )=a.
)=a.
(1)判断动点A的轨迹的形状;
(2)若直线C与动点A的轨迹有且仅有一个公共点,求实数a的值.
【答案】
(1)解:设动点A的直角坐标为(x,y),则 ![]() ,利用同角三角函数的基本关系消去参数α可得,
,利用同角三角函数的基本关系消去参数α可得,
(x﹣2)2+(y+2)2=9,点A的轨迹为半径等于3的圆.
(2)解:把直线C方程为ρcos(θ﹣ ![]() )=a化为直角坐标方程为
)=a化为直角坐标方程为 ![]() +
+ ![]() =2a,
=2a,
由题意可得直线C与圆相切,故有 ![]() =3,解得 a=3 或a=﹣3.
=3,解得 a=3 或a=﹣3.
【解析】(1)设动点A的直角坐标为(x,y),则 ![]() ,利用同角三角函数的基本关系消去参数α可得直角坐标方程,从而得到点A的轨迹.(2)把直线C方程为直角坐标方程,由题意可得直线C与圆相切,故有圆心到直线的距离等于半径,由此解得 a 的值.
,利用同角三角函数的基本关系消去参数α可得直角坐标方程,从而得到点A的轨迹.(2)把直线C方程为直角坐标方程,由题意可得直线C与圆相切,故有圆心到直线的距离等于半径,由此解得 a 的值.
【考点精析】解答此题的关键在于理解圆的参数方程的相关知识,掌握圆![]() 的参数方程可表示为
的参数方程可表示为![]() .
.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=2x,g(x)是一次函数,并且点(2,2)在函数f[(g(x)]的图象上,点(2,5)在函数g[f(x)]的图象上,则g(x)的解析式为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,曲线C1: ![]() (t为参数,t≠0),其中0≤α<π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,曲线C3:ρ=2
(t为参数,t≠0),其中0≤α<π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,曲线C3:ρ=2 ![]() cosθ.
cosθ.
(1)求C2与C3交点的直角坐标;
(2)若C2与C1相交于点A,C3与C1相交于点B,求|AB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别是a,b,c,已知c=6,sinA﹣sinC=sin(A﹣B).若1≤a≤6,则sinC的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系 且该食品在4℃的保鲜时间是16小时.
且该食品在4℃的保鲜时间是16小时.
已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示.给出以下四个结论:

①该食品在6℃的保鲜时间是8小时;
②当x∈[﹣6,6]时,该食品的保鲜时间t随着x增大而逐渐减少;
③到了此日13时,甲所购买的食品还在保鲜时间内;
④到了此日14时,甲所购买的食品已然过了保鲜时间.
其中,所有正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ax2-2ax+1+b(a>0)在区间[2,4]上的最大值为9,最小值为1,记f(x)=g(|x|)。
(1)求实数a,b的值;
(2)若不等式f(2k)>1成立,求实数k的取值范围;
(3)定义在[p,q]上的函数![]() (x),设p=x0<x1<…<xi-1<xi<…<xn=q,x1,x2,…,xn-l将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式
(x),设p=x0<x1<…<xi-1<xi<…<xn=q,x1,x2,…,xn-l将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式![]() 恒成立,则称函数
恒成立,则称函数![]() (x)为在[p,q]上的有界变差函数。试判断函数f(x)是否为在[0,4]上的有界变差函数?若是,求M的最小值;若不是,请说明理由。
(x)为在[p,q]上的有界变差函数。试判断函数f(x)是否为在[0,4]上的有界变差函数?若是,求M的最小值;若不是,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形.
的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形.
(1)求椭圆的方程;
(2)过点M分别作直线MA,MB交椭圆于A,B两点,设两直线的斜率分别为k1 , k2 , 且k1+k2=8,证明:直线AB过定点( ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 为矩形,平面
为矩形,平面![]() ,
, ![]() //
// ![]() ,
,![]() ,
, ![]() ,点
,点![]() 点P在棱
点P在棱![]() 上.
上.
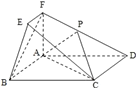
(1)求证: ![]() ;
;
(2)若![]() 是
是![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)是否存在正实数![]() ,使得
,使得![]() ,且满足二面角
,且满足二面角![]() 的余弦值为
的余弦值为![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com