
【题目】如图,四棱锥![]() 的底面
的底面![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,点
,点![]() 为
为![]() 中点.
中点.
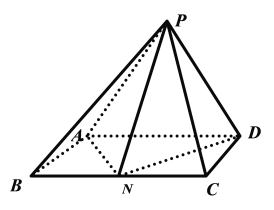
(1)证明:平面![]() 平面
平面![]() ;
;
(2)直线![]() 和平面
和平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)可证![]() 平面
平面![]() ,从而得到平面
,从而得到平面![]() 平面
平面![]() .
.
(2)设![]() 为
为![]() 中点,连结
中点,连结![]() ,
,![]() ,可以证明
,可以证明![]() 、
、![]()
![]() 、
、![]() ,建立如图所示的空间直角坐标系后可求给定的二面角的余弦值.
,建立如图所示的空间直角坐标系后可求给定的二面角的余弦值.
解:(1)∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]()
又∴![]() ,∴
,∴![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
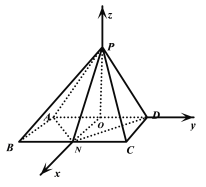
(2)设![]() 为
为![]() 中点,连结
中点,连结![]() ,
,![]() ,
,
又![]() ,故
,故![]() 且
且![]() ,
,![]() .
.
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]()
![]() ,
,
又![]() 为矩形
为矩形![]() 的对边的中点,故
的对边的中点,故![]() .
.
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 为
为![]() 轴正方向建立空间直角坐标系,
轴正方向建立空间直角坐标系,
则![]() ,
,![]() .
.
设![]() ,其中
,其中![]() ,则
,则![]() .
.
又平面![]() 的法向量为
的法向量为![]() ,
,
所以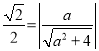 ,故
,故![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() .
.
故![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]()
故 即
即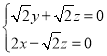 ,
,
令![]() ,∴
,∴![]() .
.
设平面![]() 的法向量为
的法向量为![]()
故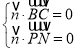 即
即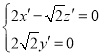 ,
,
令![]() ,∴
,∴![]() ,
,
∴![]() ,
,
因为二面角![]() 为锐角,故其余弦值为
为锐角,故其余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】北极冰融是近年来最引人注目的气候变化现象之一白色冰面融化变成颜色相对较暗的海冰,被称为“北极变暗”现象,21世纪以来,北极的气温变化是全球平均水平的2倍,被称为“北极放大”现象.如图为北极年平均海冰面积(![]() )与年平均
)与年平均![]()
![]() 浓度图.则下列说法正确的是( )
浓度图.则下列说法正确的是( )
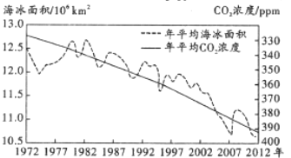
A.北极年海冰面积逐年减少
B.北极年海冰面积减少速度不断加快
C.北极年海冰面积与年平均二氧化碳浓度大体成负相关
D.北极年海冰面积与年平均二氧化碳浓度大体成正相关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】辽宁省六校协作体(葫芦岛第一高中、东港二中、凤城一中、北镇高中、瓦房店高中、丹东四中)中的某校文科实验班的![]() 名学生期中考试的语文、数学成绩都不低于
名学生期中考试的语文、数学成绩都不低于![]() 分,其中语文成绩的频率分布直方图如图所示,成绩分组区间是:
分,其中语文成绩的频率分布直方图如图所示,成绩分组区间是:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
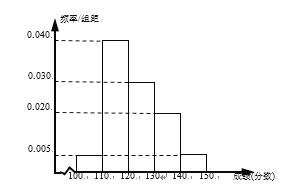
(1)根据频率分布直方图,估计这![]() 名学生语文成绩的中位数和平均数;(同一组数据用该区间的中点值作代表;中位数精确到
名学生语文成绩的中位数和平均数;(同一组数据用该区间的中点值作代表;中位数精确到![]() )
)
(2)若这![]() 名学生语文成绩某些分数段的人数
名学生语文成绩某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示:
之比如下表所示:
分组区间 |
|
|
|
|
|
|
|
|
|
从数学成绩在![]() 的学生中随机选取
的学生中随机选取![]() 人,求选出的
人,求选出的![]() 人中恰好有
人中恰好有![]() 人数学成绩在
人数学成绩在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形![]() 是梯形(如图1),
是梯形(如图1),![]() ,
,![]() ,
,![]() ,
,![]() ,E为
,E为![]() 的中点,以
的中点,以![]() 为折痕把
为折痕把![]() 折起,使点D到达点P的位置(如图2),且
折起,使点D到达点P的位置(如图2),且![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求点C到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“新冠肺炎”疫情的控制需要根据大数据进行分析,并有针对性的采取措施.下图是甲、乙两个省份从2月7日到2月13日一周内的新增“新冠肺炎”确诊人数的折线图.根据图中甲、乙两省的数字特征进行比对,下列说法错误的是( )
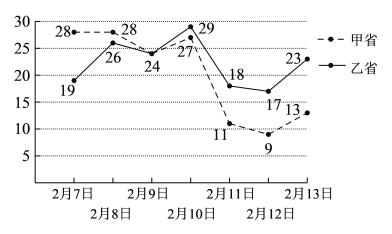
A.2月7日到2月13日甲省的平均新增“新冠肺炎”确诊人数低于乙省
B.2月7日到2月13日甲省的单日新增“新冠肺炎”确诊人数最大值小于乙省
C.2月7日到2月13日乙省相对甲省的新增“新冠甲省肺炎”确诊人数的波动大
D.后四日(2月10日至13日)乙省每日新增“新冠肺炎”确诊人数均比甲省多
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com