练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若偶函数满足，且当时，，则=（   ）
    A．B．C．－D．－
    D
    ，所以函数为周期为4的周期函数
    因为为偶函数，所以当时，，则
    因为，所以，则
    所以，故选D。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：填空题

    已知 ，猜想的表达式为        

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    函数 的图象大致是

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    设M是由满足下列条件的函数构成的集合：①方程，有实数根②函数的导数满足.
    (I) 若函数为集合M中的任意一个元素，证明：方程只有一个实数根；
    (II) 判断函数是否是集合M中的元素,并说明理由；
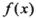    (III) 设函数为集合M中的任意一个元素，对于定义域中任意，当,且时,证明：.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    ．若函数y=f(x)的定义域是[2，4]，的定义域是（ ）
    A．[，1]B．[4，16]
    C．[]D．[2，4]

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    汕头市南澳岛有50辆自行车供游客租赁使用，管理这些自行车的费用是每日115元。根据经验，若每辆自行车的日租金不超过6元，则自行车可以全部租出；若超出6元，则每超过1元，租不出的自行车就增加3辆。为了便于结算，每辆自行车的日租金（元）只取整数，并且要求出租自行车一日的总收入必须高于这一日的管理费用，用（元）表示出租自行车的日净收入（即一日中出租自行车的总收入减去管理费用后的所得）。
    （1）求函数的解析式及其定义域；
    （2）试问当每辆自行车的日租金定为多少元时，才能使一日的净收入最多？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分13分）
    已知函数，且．(1)求实数k的值及函数的定义域；(2)判断函数在(0，＋∞)上的单调性

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知f(x)＝x7＋ax5＋bx－5，且f(－3)＝5，则f(3)＝(  　)
    A．－15B．15C．10D．－10

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    设，则f(x)+f(1-x)=______，并利用推导等差数列前n项和公式的方法，求得f(-5)+f(-4)+···+f(0)+···+f(5)+f(6)的值为________

    查看答案和解析>>

    同步练习册答案