
【题目】如图,在直角梯形![]() 中,
中,![]() ,且
,且![]() 分别为线段
分别为线段![]() 的中点,沿
的中点,沿![]() 把
把![]() 折起,使
折起,使![]() ,得到如下的立体图形.
,得到如下的立体图形.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:(1)由![]() ,结合
,结合![]() ,且
,且![]() ,所以
,所以![]() 平面
平面![]() .因为
.因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ;(2)过点
;(2)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,则
,则![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴的正方向,建立如图所示的空间直角坐标系
轴的正方向,建立如图所示的空间直角坐标系![]() ,分别根据向量垂直数量积为零列方程组求出平面
,分别根据向量垂直数量积为零列方程组求出平面![]() 与平面
与平面![]() 的一个法向量,根据空间向量夹角余弦公式,可得结果.
的一个法向量,根据空间向量夹角余弦公式,可得结果.
试题解析:(1)证明:由题可得![]() ,则
,则![]() ,
,
又![]() ,且
,且![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ;
;
(2)解:
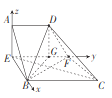
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,则
,则![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
易证![]() ,则
,则![]() ,得
,得![]() ,
,
以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴的正方向,建立如图所示的空间直角坐标系
轴的正方向,建立如图所示的空间直角坐标系![]() ,则
,则![]() .
.
故![]() ,
,
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则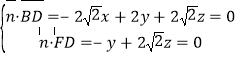 ,
,
令![]() ,得
,得![]() ,
,
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则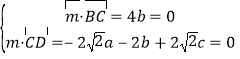 ,
,
令![]() ,则
,则![]() ,
,
因为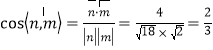 ,所以二面角
,所以二面角![]() 的余弦值为
的余弦值为![]() .
.
【方法点晴】本题主要考查利用空间向量求二面角,以及面面垂直的证明,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】如图,已知两条抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0),过原点O的两条直线l1和l2 , l1与E1 , E2分别交于A1、A2两点,l2与E1、E2分别交于B1、B2两点. 
(1)证明:A1B1∥A2B2;
(2)过O作直线l(异于l1 , l2)与E1、E2分别交于C1、C2两点.记△A1B1C1与△A2B2C2的面积分别为S1与S2 , 求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对所有高校学生进行普通话水平测试,发现成绩服从正态分布N(μ,σ2),下表用茎叶图列举出来抽样出的10名学生的成绩.
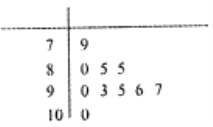
(1)计算这10名学生的成绩的均值和方差;
(2)给出正态分布的数据:P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9544.
由(1)估计从全市随机抽取一名学生的成绩在(76,97)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=x3﹣3x2+3ax﹣3a+3.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当x∈[0,2]时,求|f(x)|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)同时满足:
①对于定义域上的任意x恒有f(x)+f(﹣x)=0,
②对于定义域上的任意x1,x2,当x1≠x2时,恒有![]() 0,则称函数f(x)为“理想函数”.
0,则称函数f(x)为“理想函数”.
给出下列四个函数中①f(x)![]() ; ②f(x)
; ②f(x)![]() ; ③f(x)
; ③f(x)![]() ;④f(x)
;④f(x)![]() ,
,
能被称为“理想函数”的有_______________(填相应的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点. 
(1)证明B1C1⊥CE;
(2)求二面角B1﹣CE﹣C1的正弦值.
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为 ![]() ,求线段AM的长.
,求线段AM的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() ,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在
,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在![]() 轴下方),且线段AB的中点E在直线
轴下方),且线段AB的中点E在直线![]() 上.
上.

(1)求直线AB的方程;
(2)若点P为椭圆C上异于A、B的动点,且直线AP,BP分别交直线![]() 于点M、N,证明:OM·ON为定值.
于点M、N,证明:OM·ON为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com