
【题目】如图,正三棱柱![]() 的所有棱长均
的所有棱长均![]() ,
,![]() 为棱
为棱![]() (不包括端点)上一动点,
(不包括端点)上一动点,![]() 是
是![]() 的中点.
的中点.
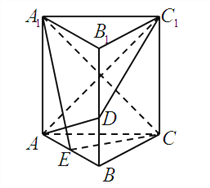
(Ⅰ)若![]() ,求
,求![]() 的长;
的长;
(Ⅱ)当![]() 在棱
在棱![]() (不包括端点)上运动时,求平面
(不包括端点)上运动时,求平面![]() 与平面
与平面![]() 的夹角的余弦值的取值范围.
的夹角的余弦值的取值范围.
【答案】(Ⅰ)BD=1;(Ⅱ)(![]() ,
,![]() ].
].
【解析】【试题分析】(I)由![]() 得到
得到![]() 平面
平面![]() ,所以
,所以![]() ,由于
,由于![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,由此得到
,由此得到![]() 为
为![]() 的中点,所以
的中点,所以![]() .(I)以
.(I)以![]() 为空间坐标原点建立空间直角坐标系,利用两个平面的法向量来求得它们夹角的余弦值的取值范围.
为空间坐标原点建立空间直角坐标系,利用两个平面的法向量来求得它们夹角的余弦值的取值范围.
【试题解析】
证明:(Ⅰ),由AC=BC,AE=BE,知CE⊥AB,
又平面ABC⊥平面ABB1A1,所以CE⊥平面ABB1A1
而AD平面ABB1A1,∴AD⊥CE,又AD⊥A1C所以AD⊥平面A1CE,
所以AD⊥A1E.易知此时D为BB1的中点,故BD=1.
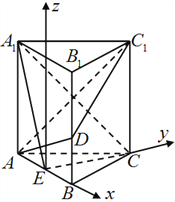
(Ⅱ)以E为原点,EB为x轴,EC为y轴,
过E作垂直于平面ABC的垂线为z轴,
建立空间直角坐标系,设BD=t,
则A(-1,0,0),D(1,0,t),C1(0,![]() ,2),
,2),
![]() =(2,0,t),
=(2,0,t),![]() =(1,
=(1,![]() ,2),设平面ADC1的法向量
,2),设平面ADC1的法向量![]() =(x,y,z),
=(x,y,z),
则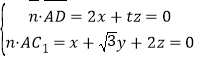 ,取x=1,得
,取x=1,得![]() ,
,
平面ABC的法向量![]() =(0,01),设平面ADC1与平面ABC的夹角为θ,
=(0,01),设平面ADC1与平面ABC的夹角为θ,
∴cosθ=![]() =
=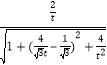 =
=![]() =
=![]()
由于t∈(0,2),故cosθ∈(![]() ,
,![]() ].
].
即平面ADC1与平面ABC的夹角的余弦值的取值范围为(![]() ,
,![]() ].
].


科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),在以坐标原点为极点,
),在以坐标原点为极点,![]() 轴非负轴为极轴的极坐标系中,曲线
轴非负轴为极轴的极坐标系中,曲线![]() :
:![]() (
(![]() 为极角).
为极角).
(1)将曲线![]() 化为极坐标方程,当
化为极坐标方程,当![]() 时,将
时,将![]() 化为直角坐标方程;
化为直角坐标方程;
(2)若曲线![]() 与
与![]() 相交于一点
相交于一点![]() ,求
,求![]() 点的直角坐标使
点的直角坐标使![]() 到定点
到定点![]() 的距离最小.
的距离最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
![]()
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前,100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
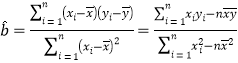 ,参考数值:
,参考数值:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为4的菱形![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,
的中点,![]() ,沿
,沿![]() 将
将![]() 翻折到
翻折到![]() ,连接
,连接![]() ,得到如图所示的五棱锥,且
,得到如图所示的五棱锥,且![]() .
.
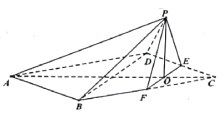
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了推动数学教学方法的改革,学校将高一年级部分生源情况基本相同的学生分成甲、乙两个班,每班各40人,甲班按原有模式教学,乙班实施教学方法改革.经过一年的教学实验,将甲、乙两个班学生一年来的数学成绩取平均数,两个班学生的平均成绩均在![]() ,按照区间
,按照区间![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.

完成表格,并判断是否有![]() 以上的把握认为“数学成绩优秀与教学改革有关”;
以上的把握认为“数学成绩优秀与教学改革有关”;

(2)从乙班![]() ,
,![]() ,
,![]() 分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自
分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自![]() 发言的人数为随机变量
发言的人数为随机变量![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018安徽江南十校高三3月联考】线段![]() 为圆
为圆![]() :
: ![]() 的一条直径,其端点
的一条直径,其端点![]() ,
, ![]() 在抛物线
在抛物线![]() :
: ![]() 上,且
上,且![]() ,
, ![]() 两点到抛物线
两点到抛物线![]() 焦点的距离之和为
焦点的距离之和为![]() .
.
(I)求直径![]() 所在的直线方程;
所在的直线方程;
(II)过![]() 点的直线
点的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
, ![]() 两点,抛物线
两点,抛物线![]() 在
在![]() ,
, ![]() 处的切线相交于
处的切线相交于![]() 点,求
点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义在R上的偶函数,对于x∈R,都有f(x+4)=f(x)+f(2)成立,当x1,x2∈[0,2]且x1≠x2时,都有![]() 给出下列四个命题:
给出下列四个命题:
①f(﹣2)=0;
②直线x=﹣4是函数y=f(x)的图象的一条对称轴;
③函数y=f(x)在[4,6]上为减函数;
④函数y=f(x)在(﹣8,6]上有四个零点.
其中所有正确命题的序号为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com