
分析 (Ⅰ)利用绝对值的几何意义,分类讨论,即可求不等式|x-3|-2|x-1|≥-1的解集;
(Ⅱ)利用基本不等式证明ab≤$(\frac{a+b}{2})^{2}$=$\frac{1}{4}$,即可证明结论.
解答 (Ⅰ)解:x<1时,-x+3+2x-2≥-1,∴x≥-2,∴-2≤x<1;
1≤x≤3时,-x+3-2x+2≥-1,∴x≤2,∴1≤x≤2;
x>3时,x-3-2x+2≥-1,∴x≤0,此时无解;
∴不等式|x-3|-2|x-1|≥-1的解集是[-2,2]…(5分)
(Ⅱ)证明:∵a,b∈R*,a+b=1,
∴ab≤$(\frac{a+b}{2})^{2}$=$\frac{1}{4}$,
∴(a+$\frac{1}{a}$)2+(b+$\frac{1}{b}$)2=4+(a2+b2)+($\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$)
=4+(1-2ab)+$\frac{1-2ab}{{a}^{2}{b}^{2}}$≥4+(1-2×$\frac{1}{4}$)+$\frac{1-2×\frac{1}{4}}{(\frac{1}{4})^{2}}$=$\frac{25}{2}$.
当且仅当a=b=$\frac{1}{2}$时不等式取等号.…(10分)
点评 本题考查不等式的解法、不等式的证明,考查基本不等式的运用,属于中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:选择题
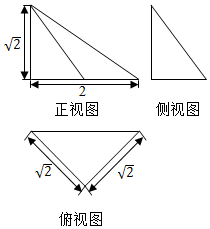
| A. | 2$\sqrt{2}$ | B. | 2+$\sqrt{2}$ | C. | 2+2$\sqrt{2}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{1000}$ | B. | $\frac{1}{1003}$ | C. | $\frac{50}{1000}$ | D. | $\frac{50}{1003}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校从参加高三模拟考试的学生中随机抽取60名学生,按其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图中的信息,回答下列问题:
某校从参加高三模拟考试的学生中随机抽取60名学生,按其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图中的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com