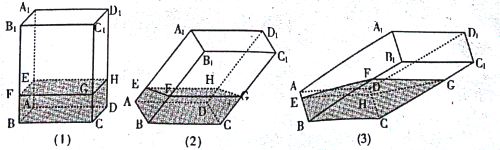
【题目】如图，透明塑料制成的长方体ABCD﹣A1B1C1D1内灌进一些水，固定容器底面一边BC于水平地面上，再将容器倾斜，随着倾斜度不同，有下面五个命题：
①有水的部分始终呈棱柱形；
②没有水的部分始终呈棱柱形；
③水面EFGH所在四边形的面积为定值；
④棱A1D1始终与水面所在平面平行；
⑤当容器倾斜如图(3)所示时，BEBF是定值．
其中所有正确命题的序号是 ____．
科学实验活动册系列答案科目：高中数学 来源： 题型：
【题目】已知某运动员每次投篮命中的概率都为
，现采用随机模拟的方法估计该运动员三次投篮都命中的概率：先由计算机产生0到9之间取整数值的随机数，指定1，2，3，4，5表示命中；6，7，8，9，0表示不命中，再以每三个随机数为一组，代表三次投篮的结果，经随机模拟产生了如下20组随机数：
162 966 151 525 271 932 592 408 569 683
471 257 333 027 554 488 730 163 537 989
据此估计，该运动员三次投篮都命中的概率为
A. 0.15 B. 0.2 C. 0.25 D. 0.35
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知四棱锥P—ABCD，底面ABCD是边长为4的菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC、PC的中点．
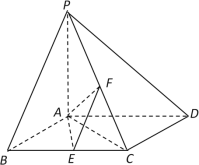
（Ⅰ）求证：AE⊥PD；
（Ⅱ）若PA=4，求二面角E—AF—C的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】通常用
、
、
分别表示
的三个内角
、
、
所对的边长，
表示的外接圆半径.
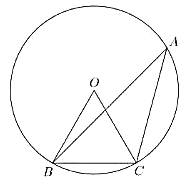
（1）如图，在以
为圆心，半径为
的圆中，
、
是圆的弦，其中
，
，角是锐角，求弦的长；
（2）在中，若
是钝角，求证：
；
（3）给定三个正实数、、，其中
，问、、满足怎样的关系时，以、为边长，为外接圆半径的不存在、存在一个或存在两个（全等的三角形算作同一个）？在存在的情况下，用、、表示.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】现有4个人去参加某娱乐活动，该活动有甲、乙两个游戏可供参加者选择．为增加趣味性，约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏，掷出点数为1或2的人去参加甲游戏，掷出点数大于2的人去参加乙游戏．
(1)求这4个人中恰有2个人去参加甲游戏的概率；
(2) 用X表示这4个人中去参加乙游戏的人数，求随机变量X的分布列与数学期望E（X）．
查看答案和解析>>
科目：高中数学 来源： 题型：
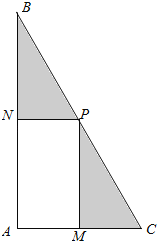
【题目】某学校为进行“阳光运动一小时”活动，计划在一块直角三角形
的空地上修建一个占地面积为
（平方米）的矩形
健身场地。如图，点
在
上，点
在
上，且
点在斜边
上，已知
米，
米，
，设矩形健身场地每平方米的造价为
元，再把矩形以外（阴影部分）铺上草坪，每平方米的造价为
元（
为正的常数）.
（1）试用
表示，并指出如何设计矩形的长和宽，才能使得矩形的面积最大，且求出的最大值；
（2）求总造价
关于面积的函数
，说明如何选取
，使总造价最低（不要求求出最低造价）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【2018届天津市耀华中学高三上学期第三次月考】已知椭圆
的一个焦点在直线
上，且离心率
.
（1）求该椭圆的方程；
（2）若
与
是该椭圆上不同的两点，且线段
的中点
在直线
上，试证： 
轴上存在定点
，对于所有满足条件的
与
，恒有
；
（3）在（2）的条件下， 
能否为等腰直角三角形？并证明你的结论.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线的顶点在原点,过点A(-4,4)且焦点在x轴.
（1）求抛物线方程;
（2）直线l过定点B(-1,0)与该抛物线相交所得弦长为8,求直线l的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某商场购进一种每件价格为90元的新商品，在商场试销时发现：销售单价
（元/件）与每天销售量
（件）之间满足如图所示的关系．
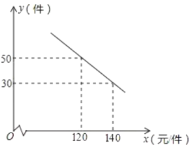
（1）求出与之间的函数关系式；
（2）写出每天的利润
与销售单价之间的函数关系式，并求出售价定为多少时，每天获得的利润最大？最大利润是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
