
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,O为AC的中点.
,O为AC的中点.
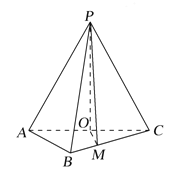
(1)证明:![]() 平面ABC;
平面ABC;
(2)若点M在棱BC上,且![]() ,求点C到平面POM的距离.
,求点C到平面POM的距离.
(3)若点M在棱BC上,且二面角![]() 为30°,求PC与平面PAM所成角的正弦值.
为30°,求PC与平面PAM所成角的正弦值.
【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】
(1)由条件![]() , O为AC的中点可得
, O为AC的中点可得![]() ,同理
,同理![]() ,求出
,求出![]() 的三边长,利用勾股定理可得
的三边长,利用勾股定理可得![]() ,从而可证.
,从而可证.
(2)由(1)可知,平面![]() 平面ABC,作
平面ABC,作![]() ,垂足为H,所以
,垂足为H,所以![]() 平面POM.所以
平面POM.所以![]() 的长度为点C到平面POM的距离,然后通过解三角形解出
的长度为点C到平面POM的距离,然后通过解三角形解出![]() 即可.
即可.
(3)以O为坐标原点,![]() ,
,![]() ,
,![]() 的分别为x,
的分别为x,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,平面PAC的一个法向量
,平面PAC的一个法向量![]()
![]() ,设
,设![]() ,求出平面PAM的法向量为
,求出平面PAM的法向量为![]() ,由
,由![]() ,可求出
,可求出![]() 的值,从而可求出PC与平面PAM所成角的正弦值.
的值,从而可求出PC与平面PAM所成角的正弦值.
证明:因为![]() ,O为AC的中点,所以
,O为AC的中点,所以![]() ,且
,且![]() .
.
连接OB.因为![]() ,
,
所以![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,
由![]() 知,
知,![]() .
.
由![]() ,
,![]() 且
且![]() ,知
,知![]() 平面ABC.
平面ABC.
(2)解:作![]() ,垂足为H.
,垂足为H.
又由(1)可得![]() ,所以
,所以![]() 平面POM.
平面POM.
故CH的长为点C到平面POM的距离.
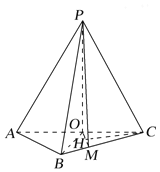
由题设可知![]() ,
,![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,![]()
所以![]() ,则
,则![]() ,
,
即![]()
又![]() ,
,
所以![]() .
.
所以点C到平面POM的距离为![]() .
.
(3)解:如图,以O为坐标原点,![]() ,
,![]() ,
,![]() 的分别为x,
的分别为x,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
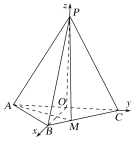
由已知得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
取平面PAC的一个法向量![]()
![]() .
.
在平面![]() 内直线
内直线![]() 的平面直角坐标方程为:
的平面直角坐标方程为:![]() ,
,
设![]() (
(![]() ),则
),则![]()
![]() .
.![]() ,
,
设平面PAM的法向量为![]() .
.
由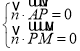 ,得
,得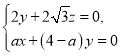
可取![]() ,
,
所以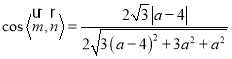 .
.
由已知可得![]() ,
,
所以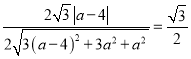 ,解得
,解得![]() (舍去),
(舍去),![]() ,
,
所以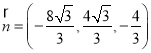 .
.
又![]() ,所以
,所以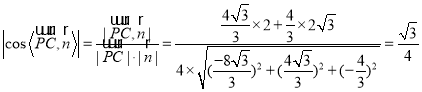 .
.
所以PC与平面PAM所成角的正弦值为![]() .
.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】设![]() 是函数
是函数![]() 定义域的一个子集,若存在
定义域的一个子集,若存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 是
是![]() 的一个“准不动点”,也称
的一个“准不动点”,也称![]() 在区间
在区间![]() 上存在准不动点,已知
上存在准不动点,已知![]() ,
,![]() .
.
(1)若![]() ,求函数
,求函数![]() 的准不动点;
的准不动点;
(2)若函数![]() 在区间
在区间![]() 上存在准不动点,求实数
上存在准不动点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Tn为数列{an}的前n项的积,即Tn=a1a2…an.
(1)若Tn=n2,求数列{an}的通项公式;
(2)若数列{an}满足Tn=![]() (1﹣an)(n∈N*),证明数列
(1﹣an)(n∈N*),证明数列![]() 为等差数列,并求{an}的通项公式;
为等差数列,并求{an}的通项公式;
(3)数列{an}共有100项,且满足以下条件:
①![]() ;
;
②![]() (1≤k≤99,k∈N*).
(1≤k≤99,k∈N*).
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)试问符合条件的数列共有多少个?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过抛物线![]() 焦点
焦点![]() 的直线与抛物线交于
的直线与抛物线交于![]() (其中
(其中![]() 点在
点在![]() 轴的上方)两点.
轴的上方)两点.
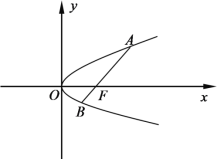
(1)若线段![]() 的长为3,求
的长为3,求![]() 到直线
到直线![]() 的距离;
的距离;
(2)证明:![]() 为钝角三角形;
为钝角三角形;
(3)已知![]() 且
且![]() ,求三角形
,求三角形![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在半径为![]() 的球内有一内接正三棱锥,它的底面三个顶点恰好都在同一个大圆上,一个动点从三棱锥的一个顶点出发沿球面运动,经过其余三点后返回,则经过的最短路程是________
的球内有一内接正三棱锥,它的底面三个顶点恰好都在同一个大圆上,一个动点从三棱锥的一个顶点出发沿球面运动,经过其余三点后返回,则经过的最短路程是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a∈R,函数f(x)=x|x-a|-a.
(1) 若f(x)为奇函数,求a的值;
(2) 若对任意的x∈[2,3],f(x)≥0恒成立,求a的取值范围;
(3) 当a>4时,求函数y=f(f(x)+a)零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
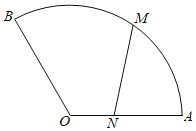
【题目】某公园草坪上有一扇形小径(如图),扇形半径为![]() ,中心角为
,中心角为![]() ,甲由扇形中心
,甲由扇形中心![]() 出发沿
出发沿![]() 以每秒2米的速度向
以每秒2米的速度向![]() 快走,同时乙从
快走,同时乙从![]() 出发,沿扇形弧以每秒
出发,沿扇形弧以每秒![]() 米的速度向
米的速度向![]() 慢跑,记
慢跑,记![]() 秒时甲、乙两人所在位置分别为
秒时甲、乙两人所在位置分别为![]() ,
,![]() ,通过计算
,通过计算![]() ,判断下列说法是否正确:
,判断下列说法是否正确:
(1)当![]() 时,函数
时,函数![]() 取最小值;
取最小值;
(2)函数![]() 在区间
在区间![]() 上是增函数;
上是增函数;
(3)若![]() 最小,则
最小,则![]() ;
;
(4)![]() 在
在![]() 上至少有两个零点;
上至少有两个零点;
其中正确的判断序号是______(把你认为正确的判断序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(I)证明:CE∥平面PAB;
(II)求直线CE与平面PBC所成角的正弦值

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,定义![]() 为两点
为两点![]() 、
、![]() 的“切比雪夫距离”,又设点
的“切比雪夫距离”,又设点![]() 及
及![]() 上任意一点
上任意一点![]() ,称
,称![]() 的最小值为点
的最小值为点![]() 到直线
到直线![]() 的“切比雪夫距离”,记作
的“切比雪夫距离”,记作![]() ,给出四个命题,正确的是________.
,给出四个命题,正确的是________.
①对任意三点![]() 、
、![]() 、
、![]() ,都有
,都有![]() ;
;
② 到原点的“切比雪夫距离”等于![]() 的点的轨迹是正方形;
的点的轨迹是正方形;
③ 已知点![]() 和直线
和直线![]() ,则
,则![]() ;
;
④ 定点![]() 、
、![]() ,动点
,动点![]() 满足
满足![]() ,则点
,则点![]() 的轨迹与直线
的轨迹与直线![]() (
(![]() 为常数)有且仅有
为常数)有且仅有![]() 个公共点.
个公共点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com