
【题目】某校高一、高二年级的全体学生都参加了体质健康测试,测试成绩满分为100分,规定测试成绩在![]() 之间为“体质优秀”,在
之间为“体质优秀”,在![]() 之间为“体质良好”,在
之间为“体质良好”,在![]() 之间为“体质合格”,在
之间为“体质合格”,在![]() 之间为“体质不合格”.现从这两个年级中各随机抽取7名学生,测试成绩如下:
之间为“体质不合格”.现从这两个年级中各随机抽取7名学生,测试成绩如下:

其中m,n是正整数.
(Ⅰ)若该校高一年级有280学生,试估计高一年级“体质优秀”的学生人数;
(Ⅱ)若从高一年级抽取的7名学生中随机抽取2人,记X为抽取的2人中为“体质良好”的学生人数,求X的分布列及数学期望;
(Ⅲ)设两个年级被抽取学生的测试成绩的平均数相等,当高二年级被抽取学生的测试成绩的方差最小时,写出m,n的值.(只需写出结论)
【答案】(Ⅰ)120人;(Ⅱ)分布列见解析,![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ )高一年级随机抽取的7名学生中,“体质优秀”的有3人,优秀率为![]() ,即可算出答案
,即可算出答案
(Ⅱ)高一年级抽取的7名学生中“体质良好”的有2人,非“体质良好”的有5人.所以X的可能取值为0,1,2,然后分别算出对应的概率即可
(Ⅲ)高一年级被抽取学生的测试成绩的平均数为![]() ,故高二年级被抽取学生的测试成绩的平均数也为
,故高二年级被抽取学生的测试成绩的平均数也为![]() ,从而可得
,从而可得![]() ,所以要使方差最小,
,所以要使方差最小,![]() .
.
(Ⅰ)高一年级随机抽取的7名学生中,“体质优秀”的有3人,优秀率为![]() ,将此频率视为概率,估计高一年级“体质优秀”的学生人数为
,将此频率视为概率,估计高一年级“体质优秀”的学生人数为![]() .
.
(Ⅱ)高一年级抽取的7名学生中“体质良好”的有2人,非“体质良好”的有5人.所以X的可能取值为0,1,2
所以![]() ,
,![]() ,
,![]()
所以随机变量X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
![]()
(Ⅲ)![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某厂加工的零件按箱出厂,每箱有10个零件,在出厂之前需要对每箱的零件作检验,人工检验方法如下:先从每箱的零件中随机抽取4个零件,若抽取的零件都是正品或都是次品,则停止检验;若抽取的零件至少有1个至多有3个次品,则对剩下的6个零件逐一检验.已知每个零件检验合格的概率为0.8,每个零件是否检验合格相互独立,且每个零件的人工检验费为2元.
(1)设1箱零件人工检验总费用为![]() 元,求
元,求![]() 的分布列;
的分布列;
(2)除了人工检验方法外还有机器检验方法,机器检验需要对每箱的每个零件作检验,每个零件的检验费为1.6元.现有1000箱零件需要检验,以检验总费用的数学期望为依据,在人工检验与机器检验中,应该选择哪一个?说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 上任意一点到两个焦点的距离和为4,且离心率为
上任意一点到两个焦点的距离和为4,且离心率为![]() .
.
(1)求椭圆![]() 的方程.
的方程.
(2)过![]() 作互相垂直的两条直线分别与椭圆
作互相垂直的两条直线分别与椭圆![]() 交于
交于![]() ,
,![]() 和
和![]() ,
,![]() ,设
,设![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,试探究直线
,试探究直线![]() 是否过定点?若是,求出该定点;若不是,说明理由.
是否过定点?若是,求出该定点;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 过椭圆
过椭圆![]() 的焦点,且椭圆
的焦点,且椭圆![]() 的中心
的中心![]() 关于直线
关于直线![]() 的对称点的横坐标为
的对称点的横坐标为![]() (
(![]() 为椭圆
为椭圆![]() 的焦距).
的焦距).
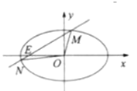
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在过点![]() ,且交椭圆
,且交椭圆![]() 于点
于点![]() 的直线
的直线![]() ,满足
,满足![]() .若存在,求直线
.若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某款电视机的寿命,研究人员对该款电视机进行了相应的测试,将得到的数据分组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并统计如图所示:
,并统计如图所示:
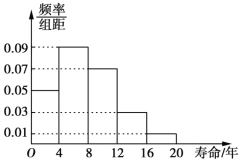
并对不同性别的市民对这款电视机的购买意愿作出调查,得到的数据如下表所示:
愿意购买该款电视机 | 不愿意购买该款电视机 | 总计 | |
男性 | 800 | 1000 | |
女性 | 600 | ||
总计 | 1200 |
(1)根据图中的数据,试估计该款电视机的平均寿命;
(2)根据表中数据,能否在犯错误的概率不超过0.001的前提下认为“是否愿意购买该款电视机”与“市民的性别”有关;
(3)以频率估计概率,若在该款电视机的生产线上随机抽取4台,记其中寿命不低于4年的电视机的台数为X,求X的分布列及数学期望.
参考公式及数据: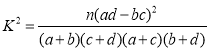 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的![]() ,
,![]() ,
,![]() 三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
车间 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自![]() ,
,![]() ,
,![]() 各车间产品的数量;
各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件产品来自相同车间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 是坐标原点,
是坐标原点,![]() 为抛物线上的一点,向量
为抛物线上的一点,向量![]() 与
与![]() 轴正方向的夹角为60°,且
轴正方向的夹角为60°,且![]() 的面积为
的面积为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若抛物线![]() 的准线与
的准线与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,求当
上,求当![]() 取得最大值时,直线
取得最大值时,直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着食品安全问题逐渐引起人们的重视,有机、健康的高端绿色蔬菜越来越受到消费者的欢迎,同时生产—运输—销售一体化的直销供应模式,不仅减少了成本,而且减去了蔬菜的二次污染等问题.
(1)在有机蔬菜的种植过程中,有机肥料使用是必不可少的.根据统计某种有机蔬菜的产量与有机肥料的用量有关系,每个有机蔬菜大棚产量的增加量![]() (百斤)与使用堆沤肥料
(百斤)与使用堆沤肥料![]() (千克)之间对应数据如下表
(千克)之间对应数据如下表
使用堆沤肥料 | 2 | 4 | 5 | 6 | 8 |
产量的增加量 | 3 | 4 | 4 | 4 | 5 |
依据表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;并根据所求线性回归方程,估计如果每个有机蔬菜大棚使用堆沤肥料10千克,则每个有机蔬菜大棚产量增加量
;并根据所求线性回归方程,估计如果每个有机蔬菜大棚使用堆沤肥料10千克,则每个有机蔬菜大棚产量增加量![]() 是多少百斤?
是多少百斤?
(2)某大棚蔬菜种植基地将采摘的有机蔬菜以每份三斤称重并保鲜分装,以每份10元的价格销售到生鲜超市.“乐购”生鲜超市以每份15元的价格卖给顾客,如果当天前8小时卖不完,则超市通过促销以每份5元的价格卖给顾客(根据经验,当天能够把剩余的有机蔬菜都低价处理完毕,且处理完毕后,当天不再进货).该生鲜超市统计了100天有机蔬菜在每天的前8小时内的销售量(单位:份),制成如下表格(注:![]() ,且
,且![]() );
);
前8小时内的销售量(单位:份) | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
频数 | 10 | x | 16 | 6 | 15 | 13 | y |
若以100天记录的频率作为每日前8小时销售量发生的概率,该生鲜超市当天销售有机蔬菜利润的期望值为决策依据,当购进17份比购进18份的利润的期望值大时,求![]() 的取值范围.
的取值范围.
附:回归直线方程为![]() ,其中
,其中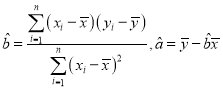 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com