
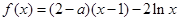 .
.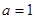 时,求
时,求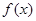 的单调区间;
的单调区间;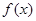 在
在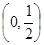 上无零点,求
上无零点,求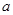 的最小值。
的最小值。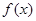 的单调递减区间为(0,2),单调递增区间为(2,
的单调递减区间为(0,2),单调递增区间为(2, ).
). 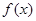 在
在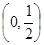 上无零点,则
上无零点,则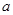 的最小值为
的最小值为 .
. 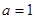 时,
时,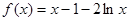 (
( ),则
),则 . 2分
. 2分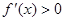 得
得 ;由
;由 得
得 . 4分
. 4分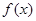 的单调递减区间为(0,2),单调递增区间为(2,
的单调递减区间为(0,2),单调递增区间为(2, ). 5分
). 5分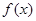 在
在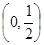 上无零点,只要对任意
上无零点,只要对任意 ,
, 无解.
无解. ,
, 无解. 7分
无解. 7分
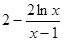 ,
, ,则
,则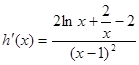 , 9分
, 9分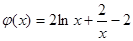 ,
, ,则
,则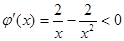 . 11分
. 11分 在
在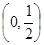 为减函数,于是
为减函数,于是
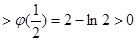 ,
,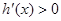 ,于是
,于是 在
在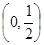 上为增函数,
上为增函数, , 13分
, 13分 无解,只要
无解,只要 .
.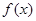 在
在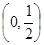 上无零点,则
上无零点,则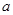 的最小值为
的最小值为 . 14分
. 14分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com