
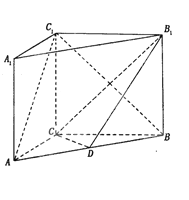
【题目】如图所示, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点,
(1)求证: AC1//平面CDB1;
(2)求二面角C1-AB-C的平面角的正切值.
【答案】(1)见解析;(3)![]()
【解析】
(1)连接DE,得DE∥AC1,由直线与平面平行的判定定理得AC1∥平面CDB1.
(2)过点C作AB的垂线CF交AB于点F,连C1F,得∠CFC1为C﹣AB﹣C1的平面角,得FC,在Rt△C1CF中得FC,解三角形即可求二面角C﹣AB﹣C1的正切值.
(1)连接DE,由题意可知:DE为△ABC1的中位线,可知DE∥AC1,由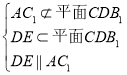 AC1∥平面CDB
AC1∥平面CDB![]() .
.
(2)过点C作AB的垂线CF交AB于点F,连C1F,∵ABC﹣A1B1C1是直三棱柱,
∴CC1⊥AB,又由AB⊥CF且CC1∩CF=C,∴AB⊥平面CFC1,∴AB⊥FC1
于是有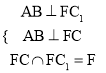 ∠CFC1为C﹣AB﹣C1的平面角,在Rt△C1CF中得FC=
∠CFC1为C﹣AB﹣C1的平面角,在Rt△C1CF中得FC=![]() =
=![]() .
.
在Rt△C1CF中,CC1=4,CF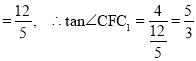 .
.
∴二面角C﹣AB﹣C1的正切值为![]() .
.


科目:高中数学 来源: 题型:
【题目】去年,相关部门对某城市“五朵金花”之一的某景区在“十一”黄金周中每天的游客人数作了统计,其频率分布如下表所示:
时间 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
频率 | 0.05 | 0.08 | 0.09 | 0.13 | 0.30 | 0.15 | 0.20 |
已知10月1日这天该景区的营业额约为8万元,假定这七天每天游客人均消费相同,则这个黄金周该景区游客人数最多的那一天的营业额约为______万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某景区内有两条道路![]() 、
、![]() ,现计划在
,现计划在![]() 上选择一点
上选择一点![]() ,新建道路
,新建道路![]() ,并把
,并把![]() 所在的区域改造成绿化区域.已知
所在的区域改造成绿化区域.已知![]() ,
,![]() ,
,![]() .若绿化区域
.若绿化区域![]() 改造成本为
改造成本为![]() 万元
万元![]() ,新建道路
,新建道路![]() 成本为
成本为![]() 万元
万元![]() .
.
(1)①设![]() ,写出该计划所需总费用
,写出该计划所需总费用![]() 的表达式,并写出
的表达式,并写出![]() 的范围;
的范围;
②设![]() ,写出该计划所需总费用
,写出该计划所需总费用![]() 的表达式,并写出
的表达式,并写出![]() 的范围;
的范围;
(2)从上面两个函数关系中任选一个,求点![]() 在何处时改造计划的总费用最小.
在何处时改造计划的总费用最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学为研究“网络游戏对当代青少年的影响”作了一次调查,共调查了50名同学,其中男生26人,有8人不喜欢玩游戏,而调查的女生中有9人喜欢玩游戏.
(1)根据以上数据完成2×2的列联表;
(2)根据以上数据,在犯错误的概率不超过0.025的前提下,能否认为“喜欢玩电脑游戏与性别有关系”?
男生 | 女生 | 总计 | |
喜欢玩游戏 | |||
不喜欢玩游戏 | |||
总计 |

| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准![]() (吨),用水量不超过
(吨),用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照![]() ,
, ![]() ,…,
,…, ![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)已知该市有80万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使![]() 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由;
的值,并说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com