
【题目】已知函数f(x)=ax﹣cosx,a≠0.
(1)若函数f(x)为单调函数,求a的取值范围;
(2)若x∈[0,2π],求:当a≥![]() 时,函数f(x)仅有一个零点.
时,函数f(x)仅有一个零点.
【答案】(1)![]() 或
或![]() (2)详见解析
(2)详见解析
【解析】
(1)首先求函数的导数,![]() ,当函数单调递增时
,当函数单调递增时![]() 恒成立,当函数单调递减时,
恒成立,当函数单调递减时,![]() 恒成立;(2)根据(1)可知当
恒成立;(2)根据(1)可知当![]() 时,函数单调递增,根据零点存在性定理可知只有一个交点,当
时,函数单调递增,根据零点存在性定理可知只有一个交点,当![]() 时,可得函数存在两个极值点,
时,可得函数存在两个极值点,![]() ,根据单调性可判断,
,根据单调性可判断,![]() 是极大值,
是极大值,![]() 是极小值,因为
是极小值,因为![]() ,
,![]() ,若函数只有一个零点,只需满足
,若函数只有一个零点,只需满足![]() ,即可求得
,即可求得![]() 的取值范围.
的取值范围.
(1)解:由![]() ,可得
,可得![]() ,
,![]() .
.
因为![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 为
为![]() 上的单调增函数;
上的单调增函数;
当![]() 时,
时,![]() ,
,![]() 为
为![]() 上的单调减函数.
上的单调减函数.
综上,若函数![]() 为单调函数,则
为单调函数,则![]() 或
或![]() .
.
(2)证明:当![]() 时,由(1)可知
时,由(1)可知![]() 为
为![]() 上的单调增函数.
上的单调增函数.
又![]() ,
,![]()
所以函数![]() 在
在![]() 有且仅有一个零点,满足题意.
有且仅有一个零点,满足题意.
当![]() 时,
时,
令![]() ,则
,则![]() .由于
.由于![]() ,所以
,所以![]() ,
,
从而必有![]() ,
,![]() ,使
,使![]() ,且
,且![]() .
.
不妨设![]() ,且有
,且有![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;
当![]() 时,
时,![]() ,
,![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,
,![]() 为增函数.
为增函数.
从而函数![]() 的极大值为
的极大值为![]() ,极小值为
,极小值为![]() .
.
因为![]() ,所以
,所以![]() ,从而极大值
,从而极大值![]() .
.
又![]() ,
,
要使函数![]() 仅有一个零点,则极小值
仅有一个零点,则极小值![]() ,
,
所以![]() ,即
,即![]() .
.
又![]() ,
,![]() ,
,
所以当![]() 时,函数
时,函数![]() 仅有一个零点.
仅有一个零点.


科目:高中数学 来源: 题型:
【题目】假设某种设备使用的年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有以下统计资料:
(万元)有以下统计资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
维修费用 | 2 | 4 | 5 | 6 | 7 |
若由资料知![]() 对
对![]() 呈线性相关关系.试求:
呈线性相关关系.试求:
(1)求![]() ;
;
(2)线性回归方程![]() ;
;
(3)估计使用10年时,维修费用是多少?
附:利用“最小二乘法”计算![]() 的值时,可根据以下公式:
的值时,可根据以下公式: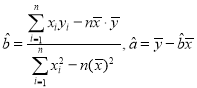
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=BC=2,P为AB边上一动点,PD∥BC交AC于点D,现将△PDA沿PD翻折至△PDA1,E是A1C的中点.
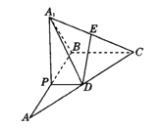
(1)若P为AB的中点,证明:DE∥平面PBA1.
(2)若平面PDA1⊥平面PDA,且DE⊥平面CBA1,求四棱锥A1﹣PBCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解春季昼夜温差大小与某种子发芽数之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了明天昼夜温差与每天100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差x/℃ | 10 | 11 | 13 | 12 | 8 |
发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
从这5天中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 君不小于25”的概率;
君不小于25”的概率;
(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5填中的另三天的数据,求出![]() 关于
关于![]() 的线性回归方程,
的线性回归方程,![]() .
.
(参考公式: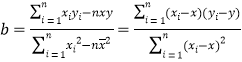 ,
,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() .
.
(1)过![]() 的直线
的直线![]() 截圆
截圆![]() 所得的弦长为
所得的弦长为![]() ,求该直线
,求该直线![]() 的斜率;
的斜率;
(2)动圆![]() 同时平分圆
同时平分圆![]() 与圆
与圆![]() 的周长.
的周长.
①求动圆圆心![]() 的轨迹方程;
的轨迹方程;
②问动圆![]() 是否过定点,若经过,则求定点坐标;若不经过,则说明理由.
是否过定点,若经过,则求定点坐标;若不经过,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆![]() 上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(1)写出C的参数方程;
(2)设直线![]() 与C的交点为
与C的交点为![]() ,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段
,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段![]() 的中点且与
的中点且与![]() 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中错误的是
A. 若命题p为真命题,命题q为假命题,则命题“pV(q)”为真命题
B. 命题“若a+b≠7,则a≠2或b≠5”为真命题
C. 命题“若x2-x=0,则x=0或x=1”的否命题为“若x2-x=0,则x≠0且x≠1”
D. 命题p: ![]() x>0,sinx>2x-1,则
x>0,sinx>2x-1,则![]() p为
p为![]() x>0,sinx≤2x-1
x>0,sinx≤2x-1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2016年8月巴西里约热内卢举办的第31届奥运会上,乒乓球比赛团体决赛实行五场三胜制,且任何一方获胜三场比赛即结束.甲、乙两个代表队最终进入决赛,根据双方排定的出场顺序及以往战绩统计分析,甲队依次派出的五位选手分别战胜对手的概率如下表:
出场顺序 | 1号 | 2号 | 3号 | 4号 | 5号 |
获胜概率 |
|
|
|
|
|
若甲队横扫对手获胜(即3∶0获胜)的概率是![]() ,比赛至少打满4场的概率为
,比赛至少打满4场的概率为![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)求甲队获胜场数的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com