已知函数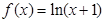
满足0＜
＜1。
（1）求
的取值范围；
（2）若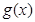
是偶函数且满足
，当
时，有
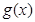，求 在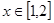
上的解析式。
科目：高中数学 来源： 题型：解答题
商店出售茶壶和茶杯，茶壶单价为每个20元，茶杯单价为每个5元，该店推出两种促销优惠办法：
（1）买1个茶壶赠送1个茶杯；
（2）按总价打9.2折付款。
某顾客需要购买茶壶4个，茶杯若干个，（不少于4个），若设购买茶杯数为x个，付款数为y（元），试分别建立两种优惠办法中y与x之间的函数关系式，并讨论该顾客买同样多的茶杯时，两种办法哪一种更省钱？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分12分）
某商品在近30天内每天的销售价格P（元）与时间t（天）的函数关系式为：
P＝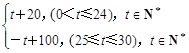
；该商品的日销售量Q（件）与时间（天）的函数关系式为：
Q＝－t＋40（0＜t≤30，t∈N*）．求这种商品日销售金额的最大值，并指出日销售金额最大的一天是30天中的哪一天？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知集合M是满足下列性质的函数f(x)的全体：存在非零常数T，对任意x∈R，有f(x+T)="T" f(x)成立.
（Ⅰ）函数f(x)=" x" 是否属于集合M？说明理由；
（Ⅱ）设函数f(x)=ax（a>0,且a≠1）的图象与y=x的图象有公共点，证明：f(x)=ax∈M；
（Ⅲ）若函数f(x)=sinkx∈M ,求实数k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
；（2）当
时，
。
，解得：
，-x+2
,所以
，所以g(x)=g(-x)=
的图象经过点（2，
），其中
且
。
的值；
，解关于
的不等式
。
满足
，且该函数的图像与
轴交于点
，在
轴上截得的线段长为
。
时，求
和日产量
均为价格
的函数，且
，日成本C关于日产量
时的价格为均衡价格，求均衡价格
最大，求
.
，分别求
的值；
的图像，并指出函数的单调区间（不要求证明）；
,
,
,求
取值范围; 
的最值，并给出函数取最值时对应的x的值。