Question

【题目】已知平面上动点到点的距离与到直线的距离之比为，记动点的轨迹为曲线.

（1）求曲线的方程；

（2）设是曲线上的动点，直线的方程为.

①设直线与圆交于不同两点， ，求的取值范围；

②求与动直线恒相切的定椭圆的方程；并探究：若是曲线： 上的动点，是否存在直线： 恒相切的定曲线？若存在，直接写出曲线的方程；若不存在，说明理由.

Answer 1

【答案】（1）；（2）见解析

【解析】分析：（1）设设，根据动点到点的距离与到直线的距离之比为，建立方程，即可求得曲线的方程；（2）①先求出圆心到直线的距离，结合勾股定理可表示出，再根据及，即可求得的取值范围，从而可得的取值范围；②取， ，直线的方程为，取， 时，直线的方程为，根据椭圆对称性，猜想的方程为与直线相切，由此联立方程组，转化为恒成立，即可推出存在，若是曲线： 上的动点，结合以上结论可得与直线相切的定曲线的方程为.

详解：（1）设，由题意，得.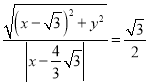

整理，得，所以曲线的方程为.

（2）①圆心到直线的距离

∵直线于圆有两个不同交点，

∴

又∵

∴

由，得.

又∵

∴

∴

因此， ，即的取值范围为.

②当， 时，直线的方程为；当， 时，直线的方程为，根据椭圆对称性，猜想的方程为.

下证：直线与相切，其中，即.

由消去得： ，即.

∴恒成立，从而直线与椭圆： 恒相切.

若点是曲线： 上的动点，则直线： 与定曲线： 恒相切.