
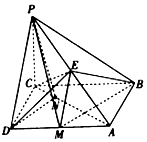
 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是矩形,BC=PC,E是PA的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是矩形,BC=PC,E是PA的中点.分析 (1)取PB的中点为F,连接CF和EF,证明DC⊥PB,CF⊥PB,即可证明平面PBM⊥平面CDE;
(2)利用VN-DCE=VE-DCN,能求出点N到平面CDE的距离.
解答 证明:(1)取PB的中点为F,连接CF和EF,
∵E是PA的中点,∴EF∥AB∥DC,
∴平面CDE与平面CDEF为同一平面,
∵PC⊥底面ABCD,底面ABCD是矩形,
∴DCPC,DC⊥BC,即DC⊥平面PBC,∴DC⊥PB.
∵BC=PC,∴CF⊥PB,
∵CD∩CF=C,∴PB⊥平面CDE.
∵PB?平面PBM,∴平面PBM⊥平面CDE.
(2)解:过D作DG∥BM交BC于G,连接PG,
∵M是AD的中点,∴EM∥PD,
∵PD∩DG=D,∴平面PDG∥平面BEM,
∴当N是AC与DG的交点时,平面PDN∥平面BEM,
在矩形ABCD中,由已知得$\frac{CN}{AN}$=$\frac{CG}{AD}$=$\frac{1}{2}$,
∵BC=2AB=4,∴S△DCN=$\frac{1}{3}$,S△DCN=2$\sqrt{2}$,
E到平面ABCD的距离为2,设点N到平面CDE的距离为d,
由VN-DCE=VE-DCN得$\frac{1}{3}$×$2\sqrt{2}d$=$\frac{1}{3}×2×\frac{4}{3}$,解得d=$\frac{2\sqrt{2}}{3}$.
点评 本题考查线面垂直的判定,考查等体积法求点到平面的距离,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | $\frac{3}{2}$+$\sqrt{2}$ | C. | 3$\sqrt{2}$+2 | D. | 2$\sqrt{2}$+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
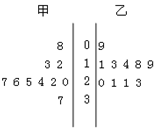 某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数的茎叶图如图所示,则下列结论错误 的一个是( )
某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数的茎叶图如图所示,则下列结论错误 的一个是( )| A. | 甲的极差是29 | B. | 甲的中位数是25 | ||
| C. | 乙的众数是21 | D. | 甲的平均数比乙的大 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
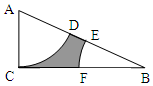 如图,在Rt△ACB中,∠ACB=90°,BC=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BEF,D、E在AB上,F在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )
如图,在Rt△ACB中,∠ACB=90°,BC=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BEF,D、E在AB上,F在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )| A. | $\frac{π}{8}$ | B. | 1-$\frac{π}{8}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com