Question

【题目】现有边长分别3，4，5的三角形两个，边长分别4，5，的三角形四个，边长分别为，4，5的三角形六个.用上述三角形为面，可以拼成______个四面体.

Answer 1

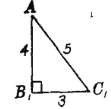
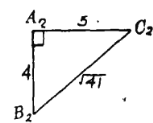
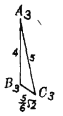
【答案】一

【解析】

如图所示，.

能拼成四面体的关键之一是两相邻面的交棱长相等，关键之二是每顶点处任两个面角之和大于第三个面角.据题设条件知，每种三角形必须成对出现.不仿设拼成的四面体为PQRS，如图.

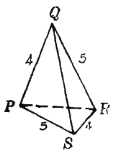
（1）若取两个置于和上，使.

（i）若取两个置于和上，（），则P处的三个面角分别为和.而，所以不能拼成四面体.

（ii）若取另两个置于和上，（）则P处的三个面角分别和，而

（可用余弦定理算之），所以也不能拼成四面体.

（iii）若取两个置于和上（），则P处的三个面角分别和，而（因为

，且内为减函数），所以仍不能拼成.

（2）若取两个置于和上，使.

（i）若取两个另置于两个面上（），由上述（1）、（iii）知不能拼成四面体.

（ii）若取两个置于另两个面上（），则P处的三个面角分别和，而，因此也不能拼成.

（iii）若取另两个置于另两个面上（），则P处的三个面角分别和，而其中最大角（因为，且在内为增函数），即顶点处的三个面角任二个面角之和大于第三个面角成立.

所以，这四个三角形仅能拼成一个四面体.