
【题目】在如图所示的五面体ABCDEF中,AB∥CD,AB=2AD=2,∠ADC=∠BCD=120°,四边形EDCF是正方形,二面角E﹣DC﹣A的大小为90°.
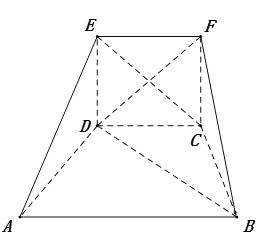
(1)求证:直线AD⊥平面BDE
(2)求点D到平面ABE的距离.
【答案】(1)证明见解析 (2)![]() .
.
【解析】
(1)先证明ED⊥AD,再由余弦定理得BD![]() ,根据勾股定理证明AD⊥BD得到证明.
,根据勾股定理证明AD⊥BD得到证明.
(2)利用等体积法VE﹣ABD=VD﹣ABE,得到![]() 计算得到答案.
计算得到答案.
(1)证明:因为四边形EDCF为正方形,所以ED⊥CD
因为二面角E﹣DC﹣A的大小为90°,所以平面EDCF⊥平面ABCD,
由面面垂直的性质定理得ED⊥平面ABCD,又AD平面ABCD,
所以ED⊥AD,又因为∠ADC=120°,AB∥CD,
所以∠DAB=60°,又AB=2AD=2,
所以由余弦定理得BD![]() ,所以AD2+BD2=AB2,即AD⊥BD,
,所以AD2+BD2=AB2,即AD⊥BD,
又DE∩DB=D,DE,DB平面BDE,所以AD⊥平面BDE;
(2)设点D到平面ABE的距离为h,则VE﹣ABD=VD﹣ABE,
所以![]() 所以h
所以h![]() ,
,
所以点D到平面ABE的距离为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某高校随机抽取部分男生测试立定跳远,将成绩整理得到频率分布表如表,测试成绩在220厘米以上(含220厘米)的男生定为“合格生”,成绩在260厘米以上(含260厘米)的男生定为“优良生”.
分组(厘米) | 频数 | 频率 |
[180,200) | 0.10 | |
[200,220) | 15 | |
[220,240) | 0.30 | |
[240,260) | 0.30 | |
[260,280) | 0.20 | |
合计 | 1.00 |
(1)求参加测试的男生中“合格生”的人数.
(2)从参加测试的“合格生”中,根据表中分组情况,按分层抽样的方法抽取8名男生,再从这8名男生中抽取3名男生,记X表示3人中“优良生”的人数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前n项和
的前n项和![]() 满足
满足![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)若 (n∈N*),求数列
(n∈N*),求数列![]() 的前n项和
的前n项和![]() ;
;
(3)是否存在实数![]() 使得
使得![]() 对
对![]() 恒成立,若存在,求实数
恒成立,若存在,求实数![]() 的取值范围,若不存在说明理由.
的取值范围,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的两个焦点分别为F1,F2,离心率为
(a>b>0)的两个焦点分别为F1,F2,离心率为![]() ,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
(1)求椭圆C的方程;
(2)若直线y=kx+b与椭圆C分别交于A,B两点,且OA⊥OB,试问点O到直线AB的距离是否为定值,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.

(Ⅰ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(Ⅱ)当二面角![]() 的余弦值为
的余弦值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)已知椭圆![]() ,直线
,直线![]() 不过原点
不过原点![]() 且不平行于坐标轴,
且不平行于坐标轴,![]() 与
与![]() 有两个交点
有两个交点![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(Ⅰ)证明:直线![]() 的斜率与
的斜率与![]() 的斜率的乘积为定值;
的斜率的乘积为定值;
(Ⅱ)若![]() 过点
过点![]() ,延长线段
,延长线段![]() 与
与![]() 交于点
交于点![]() ,四边形
,四边形![]() 能否为平行四边形?若能,求此时
能否为平行四边形?若能,求此时![]() 的斜率,若不能,说明理由.
的斜率,若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足:a1=3,当n≥2时,an﹣1+an=4n;对于任意的正整数n,![]() .设{bn}的前n项和为Sn.
.设{bn}的前n项和为Sn.
(1)求数列{an}及{bn}的通项公式;
(2)求满足13<Sn<14的n的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】团体购买公园门票,票价如下表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
现某单位要组织其市场部和生产部的员工游览该公园,这两个部门人数分别为a和b![]() ,若按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;若两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为990元,那么这两个部门的人数
,若按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;若两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为990元,那么这两个部门的人数![]() ____;
____;![]() ____.
____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com