|
|
解答题:解答时要求写出必要的文字说明或推演步骤.
已知函数y=g(x)与f(x)=loga(x+1)(a>1)的图象关于原点对称.
| (1) |
|
(2) |
|
若函数F(x)=f(x)+g(x)+m为奇函数,试确定实数m的值
|
|
(3) |
|
当x∈[0,1)时,总有f(x)+g(x)≥n成立,求实数n的取值范围.
|
|
|
答案:
解析:
(1) |
解:设M(x,y)是函数y=g(x)图象上任意一点,
则M(x,y)关于原点的参考消息称点为N(-x,-y)
N在函数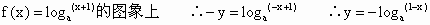 …3′ …3′
|
(2) |
解: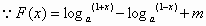 为奇函数. 为奇函数.
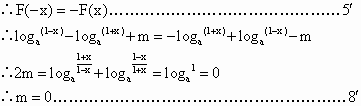
|
(3) |
解:由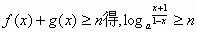

|
练习册系列答案
相关习题
科目:高中数学
来源:山东省蓬莱、牟平2006—2007学年度第一学期高三年级期中考试、数学试题(理科)
题型:044
|
|
解答题:解答时要求写出必要的文字说明或推演步骤.
已知α、β
| (1) |
|
求向量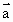 与 与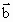 的夹角θ 的夹角θ
|
|
(2) |
|
|
查看答案和解析>>
科目:高中数学
来源:山东省蓬莱、牟平2006—2007学年度第一学期高三年级期中考试、数学试题(理科)
题型:044
|
|
解答题:解答时要求写出必要的文字说明或推演步骤.
已知f(x)=(x2+ax+a)e-x(a≤2,x∈R).
| (1) |
|
(2) |
|
是否存在实数a,使f(x)的极大值为3?若存在,求出a的值,若不存在,请说明理由.
|
|
|
查看答案和解析>>
科目:高中数学
来源:山东省蓬莱、牟平2006—2007学年度第一学期高三年级期中考试、数学试题(文科)
题型:044
|
|
解答题:解答时要求写出必要的文字说明或推演步骤.
某渔业公司年初年98万元购买一艘捕鱼船,第一年各种费用12万元,以后每年都增加4万元,每年捕鱼收益50万元.
| (1) |
|
(2) |
|
若干年后,有两种处理方案:①年平均获利最大时,以26万元出售该渔船;②总纯收入获利最大时,以8万元出售该渔船.问哪种方案最合算?
|
|
|
查看答案和解析>>
科目:高中数学
来源:山东省蓬莱、牟平2006—2007学年度第一学期高三年级期中考试、数学试题(文科)
题型:044
|
|
解答题:解答时要求写出必要的文字说明或推演步骤.
已知数列{an}的前n项和Sn满足Sn+1=KSn+2,又a1=2,a2=1.
| (1) |
|
(2) |
|
(3) |
|
已知存在正整数m、n,使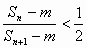 成立,试求出m、n的值. 成立,试求出m、n的值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:山东省蓬莱、牟平2006—2007学年度第一学期高三年级期中考试、数学试题(文科)
题型:044
|
|
解答题:解答时要求写出必要的文字说明或推演步骤.
已知向量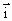 =(1,0), =(1,0),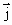 =(0,1),规定 =(0,1),规定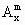 =x(x-1)……(x-m+1),其中x∈R,m∈N+,且 =x(x-1)……(x-m+1),其中x∈R,m∈N+,且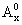 =1.函数f(x)= =1.函数f(x)=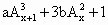 (ab≠0)在x=1处取得极值,在x=2处的切线平行向量 (ab≠0)在x=1处取得极值,在x=2处的切线平行向量 =(b+5,5a). =(b+5,5a).
| (1) |
|
(2) |
|
(3) |
|
是否存在正整数m,使得方程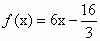 在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由. 在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.
|
|
|
查看答案和解析>>

 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案