
| 日期 | 4月6日 | 4月7日 | 4月8日 | 4月9日 | 4月10日 | 4月11日 |
| 平均气温x(℃) | 10 | 11 | 13 | 12 | 8 | 6 |
| 一天生长的长度y(mm) | 22 | 25 | 29 | 26 | 16 | 12 |
分析 (1)求出$\overline{x}$,$\overline{y}$,由公式,得$\widehat{b}$的值,从而求出$\widehat{a}$的值,从而得到y关于x的线性回归方程,
(2)由(1)能求出该小组所得线性回归方程是理想的.
解答 解:(1)∵$\overline{x}$=11,$\overline{y}$=24,
∴$\widehat{b}$=$\frac{18}{7}$,
故$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=-$\frac{30}{7}$,
故y关于x的方程是:$\widehat{y}$=$\frac{18}{7}$x-$\frac{30}{7}$;
(2)∵x=10时,$\widehat{y}$=$\frac{150}{7}$,
误差是|$\frac{150}{7}$-22|=$\frac{4}{7}$<1,
x=6时,$\widehat{y}$=$\frac{78}{7}$,误差是|$\frac{78}{7}$-12|=$\frac{6}{7}$<1,
故该小组所得线性回归方程是理想的.
点评 本题考查回归直线方程的应用,是基础题,解题时要认真审题,注意列举法的合理运用.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (0,2) | C. | [-2,2] | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
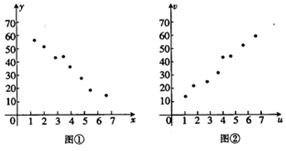 对变量x,y有观测数据(xi,yi)(i=1,2,3,…,8),得散点图如图①所示,对变量u,v有观测数据(ui,vi)(i=1,2,3,…,8),得散点图如图②所示,由这两个散点图可以判断( )
对变量x,y有观测数据(xi,yi)(i=1,2,3,…,8),得散点图如图①所示,对变量u,v有观测数据(ui,vi)(i=1,2,3,…,8),得散点图如图②所示,由这两个散点图可以判断( )| A. | 变量x与y正相关;u与v正相关 | B. | 变量x与y正相关;u与v负相关 | ||
| C. | 变量x与y负相关;u与v正相关 | D. | 变量x与y负相关;u与v负相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,面积为10的矩形中有一封闭曲线围成的阴影区域,在矩形中随机撒一粒种子,它落在阴影区域内的概率为$\frac{3}{5}$,则阴影区域的面积为6.
如图,面积为10的矩形中有一封闭曲线围成的阴影区域,在矩形中随机撒一粒种子,它落在阴影区域内的概率为$\frac{3}{5}$,则阴影区域的面积为6.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(3,+∞) | B. | (1,3) | C. | (-1,3) | D. | (-∞,1)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com