
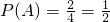 .
. .
. .
.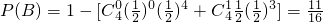 .
.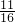 .
.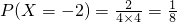 ;
; ;
;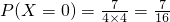 ;
;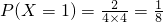 ;
; ;
; .
.| X | -2 | -1 | 0 | 1 | 2 | 4 |
| P |  |  |  |  |  |  |
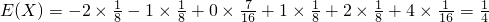 .
.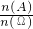 ;
; ),根据独立重复试验中某事件发生k次的概率计算公式即可求得;
),根据独立重复试验中某事件发生k次的概率计算公式即可求得;

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东华附、省高三上学期期末联考理数学卷(解析版) 题型:解答题
盒子中装有四张大小形状均相同的卡片,卡片上分别标有数 其中
其中 是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
(1)求事件 “在一次试验中,得到的数为虚数”的概率
“在一次试验中,得到的数为虚数”的概率 与事件
与事件 “在四次试验中,
“在四次试验中,
至少有两次得到虚数” 的概率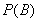 ;
;
(2)在两次试验中,记两次得到的数分别为 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望
查看答案和解析>>
科目:高中数学 来源:2013年北京市朝阳区高考数学一模试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com