
【题目】已知非零向量 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 满足
满足 ![]() =2
=2 ![]() ﹣
﹣ ![]() ,
, ![]() =k
=k ![]() +
+ ![]() ,给出以下结论:
,给出以下结论:
①若 ![]() 与
与 ![]() 不共线,
不共线, ![]() 与
与 ![]() 共线,则k=﹣2;
共线,则k=﹣2;
②若 ![]() 与
与 ![]() 不共线,
不共线, ![]() 与
与 ![]() 共线,则k=2;
共线,则k=2;
③存在实数k,使得 ![]() 与
与 ![]() 不共线,
不共线, ![]() 与
与 ![]() 共线;
共线;
④不存在实数k,使得 ![]() 与
与 ![]() 不共线,
不共线, ![]() 与
与 ![]() 共线.
共线.
其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)若![]() 和
和![]() 在区间
在区间![]() 内具有相同的单调性,求实数
内具有相同的单调性,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,且函数
,且函数![]() 的最小值为
的最小值为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义:在数列{an}中,若a ![]() ﹣a
﹣a ![]() =p(n≥2,n∈N* , p为常数),则称数列{an}为等方差数列,下列判断:
=p(n≥2,n∈N* , p为常数),则称数列{an}为等方差数列,下列判断:
①若{an}是“等方差数列”,则数列{an2}是等差数列;
②{(﹣1)n}是“等方差数列”;
③若{an}是“等方差数列”,则数列{akn}(k∈N* , k为常数)不可能还是“等方差数列”;
④若{an}既是“等方差数列”,又是等差数列,则该数列是常数列.
其中正确的结论是 . (写出所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体![]() 中,平面
中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为菱形,且
为菱形,且![]() ,
, ![]() ,
, ![]() ∥
∥![]() ,
, ![]() 为
为![]() 中点.
中点.
(Ⅰ)求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使
,使![]()
![]() ? 若存在,求
? 若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
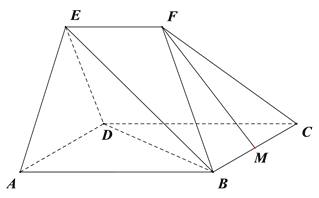
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国内,某知名连接店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖的有效展开,参与抽奖活动的人数越来越多,该分店经理对开业前7天参加抽奖活动的人数进行统计, ![]() 表示开业第
表示开业第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:

经过进一步的统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)如从这7天中随便机抽取两天,求至少有1天参加抽奖人数超过10天的概率;
(2)根据上表给出的数据,用最小二乘法,求出![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ,并估计若该活动持续10天,共有多少名顾客参加抽奖.
,并估计若该活动持续10天,共有多少名顾客参加抽奖.
参考公式: 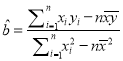 ,
, ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 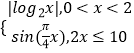 ,若存在实数x1 , x2 , x3 , x4 满足f(x1)=f(x2)=f(x3)=f(x4),且x1<x2<x3<x4 , 则
,若存在实数x1 , x2 , x3 , x4 满足f(x1)=f(x2)=f(x3)=f(x4),且x1<x2<x3<x4 , 则 ![]() 的取值范围是( )
的取值范围是( )
A.(20,32)
B.(9,21)
C.(8,24)
D.(15,25)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球2个.从袋子中不放回地随机抽取小球两个,每次抽取一个球,记第一次取出的小球标号为![]() ,第二次取出的小球标号为
,第二次取出的小球标号为![]() .
.
(1)记事件![]() 表示“
表示“![]() ”,求事件
”,求事件![]() 的概率;
的概率;
(2)在区间![]() 内任取两个实数
内任取两个实数![]() ,
,![]() ,求“事件
,求“事件![]() 恒成立”的概率.
恒成立”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某造船公司年造船量是20艘,已知造船x艘的产值函数为R(x)=3 700x+45x2-10x3(单位:万元),成本函数为C(x)=460x-5 000(单位:万元).
(1)求利润函数P(x);(提示:利润=产值-成本)
(2)问年造船量安排多少艘时,可使公司造船的年利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com