
【题目】正方体ABCD﹣A1B1C1D1 , E,F分别是上底面A1B1C1D1和侧面CDD1C1的中心,若 ![]() =x
=x ![]() +y
+y ![]() +z
+z ![]() ,则x+y+z= .
,则x+y+z= .
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】身体素质拓展训练中,人从竖直墙壁的顶点A沿光滑杆自由下滑到倾斜的木板上(人可看作质点),若木板的倾斜角不同,人沿着三条不同路径AB、AC、AD滑到木板上的时间分别为t1、t2、t3,若已知AB、AC、AD与板的夹角分别为70o、90o和105o,则( )

A. t1>t2>t3 B. t1<t2<t3 C. t1=t2=t3 D. 不能确定t1、t2、t3之间的关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间(单位:分钟)作为样本分成5组,如下表所示:
组别 | 候车时间 | 人数 |
一 | [0,5) | 2 |
二 | [5,10) | 6 |
三 | [10,15) | 4 |
四 | [15,20) | 2 |
五 | [20,25] | 1 |
(Ⅰ)求这15名乘客的平均候车时间;
(Ⅱ)估计这60名乘客中候车时间少于10分钟的人数;
(Ⅲ)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
(1)请将上表数据补充完整;函数![]() 的解析式为
的解析式为![]() (直接写出结果即可);
(直接写出结果即可);
(2)根据表格中的数据作出![]() 一个周期的图象;
一个周期的图象;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() ,
,![]() ,则函数
,则函数![]() 的图像经过怎样的变换可以得到函数
的图像经过怎样的变换可以得到函数![]() 的图像
的图像
①先向左平移![]() 个单位,再将横坐标缩短到原来的
个单位,再将横坐标缩短到原来的![]() 倍,纵坐标保持不变.
倍,纵坐标保持不变.
②先向左平移![]() 个单位,再将横坐标缩短到原来的
个单位,再将横坐标缩短到原来的![]() 倍,纵坐标保持不变.
倍,纵坐标保持不变.
③将横坐标缩短到原来的![]() 倍,再向左平移
倍,再向左平移![]() 个单位,纵坐标保持不变.
个单位,纵坐标保持不变.
④将横坐标缩短到原来的![]() 倍,再向左平移
倍,再向左平移![]() 个单位,纵坐标保持不变.
个单位,纵坐标保持不变.
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从某医院中随机抽取了7位医护人员的关爱患者考核分数(患者考核:10分制),用相关的特征量![]() 表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量
表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量![]() 表示,数据如下表:
表示,数据如下表:
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 98 | 88 | 96 | 91 | 90 | 92 | 96 |
| 9.9 | 8.6 | 9.5 | 9.0 | 9.1 | 9.2 | 9.8 |
(1)求![]() 关于
关于![]() 的线性回归方程(计算结果精确到0.01);
的线性回归方程(计算结果精确到0.01);
(2)利用(1)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计某医护人员的医护专业知识考核分数为95分时,他的关爱患者考核分数(精确到0.1)
附:回归直线方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为
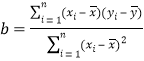 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com