
 中,已知
中,已知 ,
, ,
, .
. 与底面
与底面 所成角正切值;
所成角正切值; (不包含端点)上确定一点
(不包含端点)上确定一点 的位置,
的位置, (要求说明理由);
(要求说明理由); ,求二面角
,求二面角 的大小.
的大小.

 .
.
 ,
, ,即
,即 . ----------------------------------- 6´
. ----------------------------------- 6´  ,
,
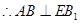 .
.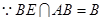
 ,
, ,
, . --- 9´
. --- 9´ 的中点
的中点 ,
, 的中点
的中点 ,则
,则 ∥
∥ ,且
,且 ,
, ,连结
,连结 ,设
,设 ,连结
,连结 ,
, ∥
∥ ,且
,且
 ,
, 为二面角
为二面角 的平面角. --------------------------- 12´
的平面角. --------------------------- 12´ ,
,  ,
,  的大小为45°. ----------------------------- 15´
的大小为45°. ----------------------------- 15´ 为原点,
为原点,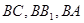 所在直线为
所在直线为 轴建立空间直角坐标系.
轴建立空间直角坐标系. . - ------------------------- 2´
. - ------------------------- 2´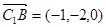 ,面
,面 的一个法向量
的一个法向量 .
. 与面
与面 所成角为
所成角为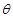 ,则
,则
 .-- 5´
.-- 5´ ,
, ,则
,则 ,
, ,
,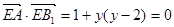 ,得
,得 ,所以
,所以 为
为 的中点. ------- 9´
的中点. ------- 9´ ,得
,得 ,
, ,又
,又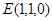 ,
, 的一个法向量
的一个法向量 ,
, 的一个法向量
的一个法向量 ,----------------------------------- 12´
,----------------------------------- 12´ 的大小为
的大小为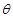 ,则
,则 .----------- 14´
.----------- 14´ 的大小为45°. ----------------------------- 15´
的大小为45°. ----------------------------- 15´

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com