
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{7}{10}$ | D. | $\frac{3}{10}$ |
分析 本题是一个等可能事件的概率,试验发生包含的事件是从10件中取1件有C101种结果,满足条件的事件是恰好有1件次品有C31种结果,得到概率即可.
解答 解:由题意知本题是一个等可能事件的概率,
试验发生包含的事件是从10件中取1件有${C}_{10}^{1}$种结果,
满足条件的事件是恰好有1件次品有${C}_{3}^{1}$种结果,
∴取到次品的概率是$\frac{{C}_{3}^{1}}{{C}_{10}^{1}}$=$\frac{3}{10}$,
故选:D.
点评 本题考查等可能事件的概率,本题解题的关键是利用组合数写出试验发生包含的事件数和满足条件的事件数,本题是一个基础题.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-1,\sqrt{2}]$ | B. | $[-\sqrt{2},\sqrt{2}]$ | C. | $[\sqrt{2}-2,2]$ | D. | $[1-\sqrt{2},1+\sqrt{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是30m,则河流的宽度BC等于( )
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是30m,则河流的宽度BC等于( )| A. | $30(\sqrt{3}-1)m$ | B. | $60(\sqrt{3}-1)m$ | C. | $90(\sqrt{3}-1)m$ | D. | $120(\sqrt{3}-1)m$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 24 | C. | 48 | D. | 720 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
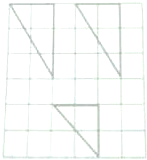 如图,网格纸上小正方体的边长为1,粗实线画出的是某多面体的三视图(第一个为主视图,下面的是俯视图),则该多面体各个面的面积最大值为$3\sqrt{2}$.
如图,网格纸上小正方体的边长为1,粗实线画出的是某多面体的三视图(第一个为主视图,下面的是俯视图),则该多面体各个面的面积最大值为$3\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com