
 如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ABC=$\frac{π}{2}$,D是棱AC的中点,且AB=BC=BB1=4.
如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ABC=$\frac{π}{2}$,D是棱AC的中点,且AB=BC=BB1=4.分析 (Ⅰ)连结CB1交BC1于点O,侧棱A1A⊥底面ABC,O为B1C的中点,且D是棱AC的中点,可得AB1∥OD,利用线面平行的判定定理即可.
(Ⅱ)AB1∥OD,可得∠DOB为异面直线AB1与BC1所成的角或其补角.解△OBD即可求出异面直线AB1与BC1所成的角.
解答 解:(Ⅰ)连结CB1交BC1于点O,…(1分)
侧棱A1A⊥底面ABC
∴侧面BB1C1C是矩形,
O为B1C的中点,且D是棱AC的中点,
∴AB1∥OD,…(3分)
∵OD平面BC1D,AB1?平面BC1D…(5分)
∴AB1∥平面BC1D…(6分)
(Ⅱ)AB1∥OD,∴∠DOB为异面直线AB1与BC1所成的角或其补角.
$∠ABC=\frac{π}{2}$,AB=BC=BB1=4$BD=2,OD=\frac{1}{2}A{B_1}=2,OB=2$,
∴△OBD为等边三角形,
∴∠DOB=60°,…(11分)
∴异面直线AB1与BC1所成的角为600.…(12分)
点评 本题考查了线面平行,异面直线所成的角,关键是要转化条件,考查学生分析解决问题的能力,难度中等.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{{\sqrt{7}}}{7}$ | C. | -1 | D. | $\frac{2\sqrt{7}}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
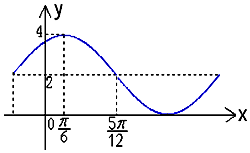 函数f(x)=Asin(ωx+ϕ)+B的一部分图象如图所示,其中A>0,ω>0,|φ|<$\frac{π}{2}$.
函数f(x)=Asin(ωx+ϕ)+B的一部分图象如图所示,其中A>0,ω>0,|φ|<$\frac{π}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5或6个 | B. | 3或9个 | C. | 9或10个 | D. | 5或9个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com