已知△
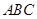
的面积
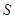
满足
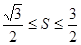
,且
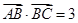
,
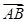
与
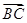
的夹角为
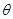
.
(1)求
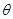
的取值范围;
(2)求函数
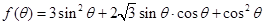
的最大值及最小值.
试题分析:(1)求
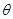
的取值范围,首先要建立与
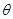
相关的不等式,应凭借条件中已有的不等式
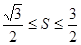
,再根据知识的内在联系,将它转换为关于
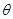
的不等式,从而求出
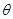
的取值范围;(2)首先应用恒等变换知识将三角函数
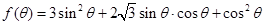
转换到特定形式:

,然后结合(1)求得的
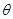
的取值范围,利用函数的单调性求其最值.
试题解析:(1)因为
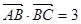
,
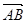
与
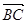
的夹角为
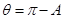
,所以


3分
又
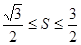
,所以
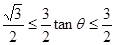
,即
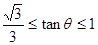
,又
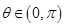
,所以

. 5分
(2)

,
因为

,所以
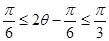
, 8分
从而当
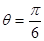
时,

的最小值为3;当
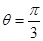
时,

的最大值为

. 12分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:填空题
将y=sin2x的图象向右按
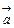
作最小的平移,使平移后的图象在[k
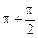
,k
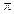
+
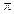
](k
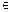
z)上递减,试求平移后的函数解析式和
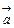
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知

、

、

是同一平面内的三个向量,其中

(1)若

,且

,求

的坐标;
(2)若

,且

与

垂直,求

与

的夹角

.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知向量
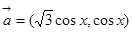
,
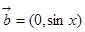
,
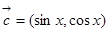
,
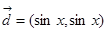
.
(1)当
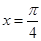
时,求向量
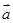
与
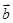
的夹角
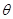
;
(2)当
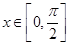
时,求
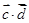
的最大值;
(3)设函数
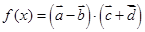
,将函数
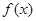
的图像向右平移
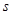
个长度单位,向上平移
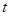
个长度单位
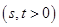
后得到函数
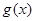
的图像,且
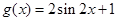
,令
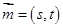
,求
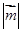
的最小值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知α是锐角,
=(
,sinα),
=(cosα,
),且
∥,则a为( )
查看答案和解析>>

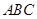 的面积
的面积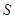 满足
满足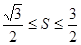 ,且
,且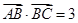 ,
,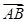 与
与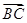 的夹角为
的夹角为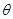 .
.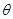 的取值范围;
的取值范围;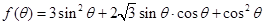 的最大值及最小值.
的最大值及最小值. 阅读快车系列答案
阅读快车系列答案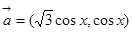 ,
,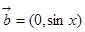 ,
,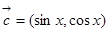 ,
,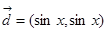 .
.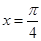 时,求向量
时,求向量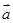 与
与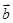 的夹角
的夹角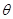 ;
;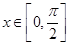 时,求
时,求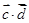 的最大值;
的最大值;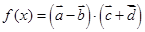 ,将函数
,将函数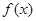 的图像向右平移
的图像向右平移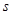 个长度单位,向上平移
个长度单位,向上平移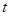 个长度单位
个长度单位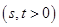 后得到函数
后得到函数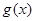 的图像,且
的图像,且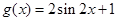 ,令
,令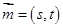 ,求
,求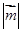 的最小值.
的最小值.