
| A. | $\frac{1}{4}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{BD}$ | B. | $\frac{1}{2}\overrightarrow{AC}+\frac{1}{4}\overrightarrow{BD}$ | C. | $\frac{1}{2}\overrightarrow{AC}+\frac{2}{3}\overrightarrow{BD}$ | D. | $\frac{2}{3}\overrightarrow{AC}+\frac{1}{3}\overrightarrow{BD}$ |
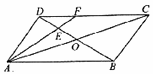
分析 根据两个三角形相似对应边成比例,得到DF与FC之比,做FG平行BD交AC于点G,使用已知向量表示出要求的向量,得到结果.
解答 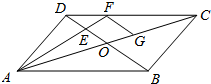 解:∵△DEF∽△BEA
解:∵△DEF∽△BEA
DF:BA═DE:BE=1:3;
作FG平行BD交AC于点G,
∴FG:DO=2:3,CG:CO=2:3,
∴$\overrightarrow{GF}$=$\frac{1}{3}$$\overrightarrow{BD}$,
∵$\overrightarrow{AG}$=$\overrightarrow{AO}$+$\overrightarrow{OG}$=$\frac{2}{3}$$\overrightarrow{AC}$,
∴$\overrightarrow{AF}$=$\overrightarrow{AG}$+$\overrightarrow{GF}$=$\frac{2}{3}\overrightarrow{AC}+\frac{1}{3}\overrightarrow{BD}$,
故选:D
点评 向量是数形结合的典型例子,向量的加减运算是用向量解决问题的基础,要学好运算,才能用向量解决立体几何问题,三角函数问题,好多问题都是以向量为载体的.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com