练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本小题满分13分）
    从5个男生，4个女生中选3人参加课外活动。
    （1）求男生甲必须参加的概率。
    （2）求男女生至少都有一名的选法有多少种。（注：结果用数字作答）
    解：（1）设男生甲必须参加为事件A
    则
    男生甲必须参加的概率是-------------------6分
    （2）男女生至少都有一名的选法有
    男女生至少都有一名的选法有70种-----------13分
    略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    1,3,5

     
     对某电子元件进行寿命追踪调查，情况如下：

    寿命（h）
    		100—200
    		200—300
    		300—400
    		400—500
    		500—600
    个数
    		20
    		30
    		80
    		40
    		30
      （1）列出频率分布表：
    （2）画频率分布直方图；
    （3）估计电子元件寿命在100h—400h以内的概率；
    （4）估计电子元件寿命在400h以上的概率.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题共13分）
    某商场在店庆日进行抽奖促销活动，当日在该店消费的顾客可参加抽奖．抽奖箱中有大小完全相同的4个小球，分别标有字“生”“意”“兴”“隆”．顾客从中任意取出1个球，记下上面的字后放回箱中，再从中任取1个球，重复以上操作，最多取4次，并规定若取出“隆”字球，则停止取球．获奖规则如下：依次取到标有“生”“意”“兴”“隆”字的球为一等奖；不分顺序取到标有“生”“意”“兴”“隆”字的球，为二等奖；取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖．
    （Ⅰ）求分别获得一、二、三等奖的概率；
    （Ⅱ）设摸球次数为，求的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
    某电视台拟举行“团队共享”冲关比赛，其规则如下：比赛共设有“常识关”和“创新关”两关，每个团队共两人，每人各冲一关，“常识关”中有2道不同必答题，“创新关”中有3道不同必答题；如果“常识关”中的2道题都答对，则冲“常识关”成功且该团队获得单项奖励900元，否则无奖励；如果“创新关”中的3道题至少有2道题答对，则冲“创新关”成功且该团队获得单项奖励1800元，否则无奖励．现某团队中甲冲击“常识关”，乙冲击“创新关”，已知甲回答“常识关”中每道题正确的概率都为，乙回答“创新关”中每道题正确的概率都为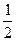，且两关之间互不影响，每道题回答正确与否相互独立．
    (I)求此冲关团队在这5道必答题中只有2道回答正确且没有获得任何奖励的概率；
    (Ⅱ)记此冲关团队获得的奖励总金额为随机变量，求的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
    日销售量
    		1
    		1.5
    		2
    频数
    		10
    		25
    		15
    频率
    		0.2
    		 
    		 
    某批发市场对某种商品的日销售量（单位：吨）进行统计，最近50天的统计结果如下：
    （Ⅰ）填充上表；
    （Ⅱ）若以上表频率作为概率，且每天的销售量相互独立.
    ①5天中该种商品恰好有2天的销售量为1.5吨的概率；
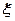    ②已知每吨该商品的销售利润为2千元，表示该种商品两天销售利润的和（单位：
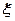    千元），求的分布列.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本题满分12分）
    甲、乙、丙三人进行象棋比赛，每两人比赛一场，共赛三场．每场比赛胜者得3
    分，负者得0分，没有平局，在每一场比赛中，甲胜乙的概率为，甲胜丙的概率为
    ，乙胜丙的概率为
    (1)求甲获第一名且丙获第二名的概率：
    (2)设在该次比赛中，甲得分为ξ，求ξ的分布列和数学期望。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    (本小题满分12分)
    盒中有个小球,个白球,记为，个红球, 记为，个黑球, 记为，除了颜色和编号外,球没有任何区别.
    (1) 求从盒中取一球是红球的概率；
    (2) 从盒中取一球，记下颜色后放回，再取一球，记下颜色，若取白球得分，取红球得分，取黑球得分，求两次取球得分之和为分的概率

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

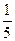    一个不透明的口袋中有若干个红球和黑球，从中摸出一个，每个球被摸出的可能
    性是相同的．现从中摸出两个球，均是红球的概率为,已知袋中红球有3个,则袋中共有球的个数为   
    A．4B．5C．6D．7

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    在一次招聘口试中，每位考生都要在5道备选试题
    中随机地抽出3道题回答，答对其中2道题即为及格．
    若一位考生只会回答5道题中的3道题，则这位考生
    能够及格的概率为　  　．

    查看答案和解析>>

    同步练习册答案