
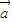 ,
,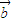 ,满足
,满足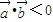 ,则
,则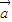 与
与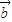 的夹角为钝角;
的夹角为钝角;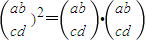 =
=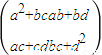 ,则
,则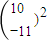 =
=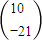
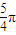 时,满足
时,满足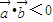 ,但不是钝角,故①错误;
,但不是钝角,故①错误;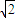 <2,
<2,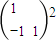 =
=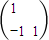
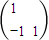 =
=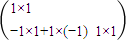 =
=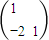


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
①若AB=AC,BD=CD,则BC⊥AD;②若AB=CD,AC=BD,则BC⊥AD;③若AB⊥AC,BD⊥CD,则BC⊥AD;④若AB⊥CD,BD⊥AC,则BC⊥AD.
其中真命题的序号是________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:河北省2009-2010学年度第二学期二调考试高一年级数学试卷理科 题型:选择题
对于四面体ABCD,给出下列四个命题:
①若AB=AC,BD=CD,则BC⊥AD; ②若AB=CD,AC=BD,则BC⊥AD;
③若AB⊥AC,BD⊥CD,则BC⊥AD; ④若AB⊥CD,AC⊥BD,则BC⊥AD;
其中正确的命题的序号是( )
A. ①② B. ②③ C. ②④ D. ①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com