
【题目】在△ABC中,D、E分别是AB、AC的中点,M是直线DE上的动点.若△ABC的面积为2,则 ![]()
![]() +
+ ![]() 2的最小值为 .
2的最小值为 . 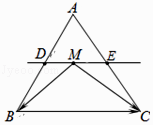
【答案】2 ![]()
【解析】解:∵D、E是AB、AC的中点, ∴M到BC的距离等于点A到BC的距离的一半,
∴S△ABC=2S△MBC , 而△ABC的面积2,则△MBC的面积S△MBC=1,
S△MBC= ![]() 丨MB丨丨MC丨sin∠BMC=1,
丨MB丨丨MC丨sin∠BMC=1,
∴丨MB丨丨MC丨= ![]() .
.
∴ ![]()
![]() =丨MB丨丨MC丨cos∠BMC=
=丨MB丨丨MC丨cos∠BMC= ![]() .
.
由余弦定理,丨BC丨2=丨BM丨2+丨CM丨2﹣2丨BM丨丨CM丨cos∠BMC,
显然,BM、CM都是正数,
∴丨BM丨2+丨CM丨2≥2丨BM丨丨CM丨,
∴丨BC丨2=丨BM丨2+丨CM丨2﹣2丨BM丨×丨CM丨cos∠BMC
=2× ![]() ﹣2×
﹣2× ![]() .
.
∴ ![]()
![]() +
+ ![]() 2≥
2≥ ![]() +2×
+2× ![]() ﹣2×
﹣2× ![]()
=2 ![]() ,
,
方法一:令y= ![]() ,则y′=
,则y′= ![]() ,
,
令y′=0,则cos∠BMC= ![]() ,此时函数在(0,
,此时函数在(0, ![]() )上单调减,在(
)上单调减,在( ![]() ,1)上单调增,
,1)上单调增,
∴cos∠BMC= ![]() 时,
时, ![]() 取得最小值为
取得最小值为 ![]() ,
,![]()
![]() +
+ ![]() 2的最小值为2
2的最小值为2 ![]() ;
;
方法二:令y= ![]() ,
,
则ysin∠BMC+cos∠BMC=2,则 ![]() sin(∠BMC+α)=2,
sin(∠BMC+α)=2,
tanα= ![]() ,
,
则sin(∠BMC+α)= ![]() ≤1,
≤1,
解得:y≥ ![]() ,
,
则 ![]()
![]() +
+ ![]() 2的最小值为2
2的最小值为2 ![]() ;
;
所以答案是:2 ![]() .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AE:EB=1:2. 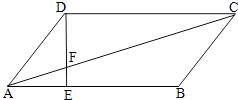
(1)求△AEF与△CDF的周长比;
(2)如果△AEF的面积等于6cm2 , 求△CDF的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆C的参数方程为 ![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为 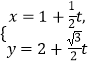 (t为参数).
(t为参数).
(Ⅰ)写出椭圆C的普通方程和直线l的倾斜角;
(Ⅱ)若点P(1,2),设直线l与椭圆C相交于A,B两点,求|PA|·|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆C的方程为ρ=2 ![]() sin
sin ![]() ,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为 ![]() (t为参数),判断直线l和圆C的位置关系.
(t为参数),判断直线l和圆C的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据,
(吨标准煤)的几组对照数据,

(1)求![]() ,
, ![]() ,
,
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技动前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
已知![]() ,
, ![]() .
.
 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国数学家科拉茨1937年提出一个著名的猜想:任给一个正整数 ![]() ,如果
,如果 ![]() 是偶数,就将它减半(即
是偶数,就将它减半(即 ![]() );如果
);如果 ![]() 是奇数,则将它乘3加1(即
是奇数,则将它乘3加1(即 ![]() ),不断重复这样的运算,经过有限步后,一定可以得到1.对于科拉茨猜想,目前谁也不能证明。也不能否定,现在请你研究:如果对正整数
),不断重复这样的运算,经过有限步后,一定可以得到1.对于科拉茨猜想,目前谁也不能证明。也不能否定,现在请你研究:如果对正整数 ![]() (首项)按照上述规则旅行变换后的第9项为1(注:1可以多次出现),则
(首项)按照上述规则旅行变换后的第9项为1(注:1可以多次出现),则 ![]() 的所有不同值的个数为 .
的所有不同值的个数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn , 数列{bn}是等比数列,满足a1=3,b1=1,b2+S2=10,a5﹣2b2=a3 .
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)令Cn= 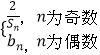 设数列{cn}的前n项和Tn , 求T2n .
设数列{cn}的前n项和Tn , 求T2n .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com