Question

【题目】某企业生产的一种电器的固定成本（即固定投资）为0.5万元，每生产一台这种电器还需可变成本（即另增加投资）25元，市场对这种电器的年需求量为5百台.已知这种电器的销售收入R与销售量t的关系可用抛物线表示，如图.

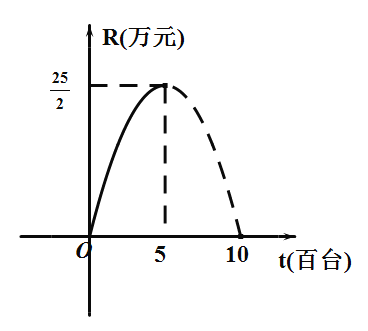
（注：销售量的单位：百台，销售收入与纯收益的单位：万元，生产成本=固定成本+可变成本，精确到1台和0.01万元）

（1）写出销售收入R与销售量t之间的函数关系式；

（2）若销售收入减去生产成本为纯收益，写出纯收益与销售量的函数关系式，并求销售量是多少时，纯收益最大.

Answer 1

【答案】（1）；（2）售量是475台时，纯收益取得最大值，为10.78万元.

【解析】

（1）根据待定系数法，得到R与销售量t的关系式，代入点，得到的值，从而得到答案；（2）设纯收益为万元，则

（1）由题图可知，

由时，，可得，

所以.

（2）设纯收益为万元，

则

，

当时，取得最大值，

故销售量是台时，纯收益取得最大值，为万元.