
【题目】已知函数![]() ,其中实数
,其中实数![]() 为常数,
为常数,![]() 为自然对数的底数.
为自然对数的底数.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() ;
;
(3)当![]() 时,如果函数
时,如果函数![]() 不存在极值点,求
不存在极值点,求![]() 的取值范围.
的取值范围.
【答案】(1)单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() .(2)
.(2)![]() (3)
(3)![]()
【解析】试题分析:把![]() 代入由于对数的真数为正数,函数定义域为
代入由于对数的真数为正数,函数定义域为![]() ,所以函数化为
,所以函数化为![]() ,求导后在定义域下研究函数的单调性给出单调区间;代入
,求导后在定义域下研究函数的单调性给出单调区间;代入![]() ,
,![]() ,分
,分![]() 和
和![]() 两种情况解不等式;当
两种情况解不等式;当![]() 时,
时,![]() ,求导
,求导![]() ,函数
,函数![]() 不存在极值点,只需
不存在极值点,只需![]() 恒成立,根据这个要求得出
恒成立,根据这个要求得出![]() 的范围.
的范围.
试题解析:
(1)![]() 时,
时,![]() ,
,
令![]() ,解得
,解得![]() ,
,
且![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
所以![]() 单调递增区间为
单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() .
.
(2)![]() 时,
时,![]() .
.
当![]() 时,原不等式可化为
时,原不等式可化为![]() .
.
记![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 单调递增,又
单调递增,又![]() ,故不等式解为
,故不等式解为![]() ;
;
当![]() 时,原不等式可化为
时,原不等式可化为![]() ,显然不成立,
,显然不成立,
综上,原不等式的解集为![]() .
.
(3)![]() 时,
时,![]() ,
,
![]() ,记
,记![]() ,
,
因为![]() 时,
时,![]() ,
,
所以![]() 不存在极值点时
不存在极值点时![]() 恒成立.
恒成立.
由![]() ,解得
,解得![]()
且![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
所以![]() ,解得
,解得![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】顶点在原点,焦点在x轴正半轴的抛物线,经过点(3,6),
(1)求抛物线截直线y=2x﹣6所得的弦长.
(2)讨论直线y=kx+1与抛物线的位置关系,并求出相应的k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过点C,已知AB=3米,AD=2米.
(Ⅰ)要使矩形AMPN的面积大于32平方米,则DN的长应在什么范围内?
(Ⅱ)当DN的长度为多少时,矩形花坛AMPN的面积最小?并求出最小值.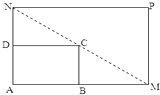
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①直线l的方向向量为 ![]() =(1,﹣1,2),直线m的方向向量
=(1,﹣1,2),直线m的方向向量 ![]() =(2,1,﹣
=(2,1,﹣ ![]() ),则l与m垂直;
),则l与m垂直;
②直线l的方向向量 ![]() =(0,1,﹣1),平面α的法向量
=(0,1,﹣1),平面α的法向量 ![]() =(1,﹣1,﹣1),则l⊥α;
=(1,﹣1,﹣1),则l⊥α;
③平面α、β的法向量分别为 ![]() =(0,1,3),
=(0,1,3), ![]() =(1,0,2),则α∥β;
=(1,0,2),则α∥β;
④平面α经过三点A(1,0,﹣1),B(0,1,0),C(﹣1,2,0),向量 ![]() =(1,u,t)是平面α的法向量,则u+t=1.
=(1,u,t)是平面α的法向量,则u+t=1.
其中真命题的是 . (把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣5x﹣6<0},集合B={x|6x2﹣5x+1≥0},集合 ![]()
(1)求A∩B;
(2)若A∪C=C,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人有楼房一幢,室内面积共计180m2 , 拟分割成两类房间作为旅游客房,大房间每间面积为18m2 , 可住游客5名,每名游客每天住宿费40元;小房间每间面积为15m2 , 可以住游客3名,每名游客每天住宿费50元;装修大房间每间需要1000元,装修小房间每间需要600元.如果他只能筹款8000元用于装修,且假定游客能住满客房,他应隔出大房间和小房间各多少间,才能获得最大收益? 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com