
ЎѕМвДїЎїДіЦРС§УРЅМК¦400ИЛЈ¬ЖдЦРёЯЦРЅМК¦240ИЛ.ОЄБЛБЛЅвёГРЈЅМК¦ГїМмїОНв¶НБ¶К±јдЈ¬ПЦАыУГ·ЦІгійСщµД·Ѕ·ЁґУёГРЈЅМК¦ЦРЛж»ъійИЎБЛ100ГыЅМК¦ЅшРРµчІйЈ¬НіјЖЖдГїМмїОНв¶НБ¶К±јд(ЛщУРЅМК¦ГїМмїОНв¶НБ¶К±јдѕщФЪ![]() ·ЦЦУДЪ)Ј¬Ѕ«НіјЖКэѕЭ°ґ
·ЦЦУДЪ)Ј¬Ѕ«НіјЖКэѕЭ°ґ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬ЎЈ¬
Ј¬ЎЈ¬![]() ·ЦіЙ6ЧйЈ¬ЦЖіЙЖµВК·ЦІјЦ±·ЅНјИзПВЈє
·ЦіЙ6ЧйЈ¬ЦЖіЙЖµВК·ЦІјЦ±·ЅНјИзПВЈє
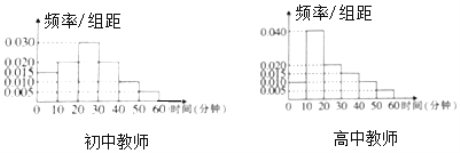
јЩЙиГїО»ЅМК¦ГїМмїОНв¶НБ¶К±јдП໥¶АБўЈ¬ІўіЖГїМм¶НБ¶К±јдРЎУЪ20·ЦЦУОЄИ±·¦¶НБ¶.
ЈЁ1Ј©КФ№АјЖ±ѕРЈЅМК¦ЦРИ±·¦¶НБ¶µДИЛКэЈ»
ЈЁ2Ј©ИфґУІОУлµчІйЈ¬ЗТГїМмїОНв¶НБ¶К±јдФЪ![]() ДЪµДёГРЈЅМК¦ЦРИОИЎ2ИЛЈ¬ЗуЦБЙЩУР1ГыіхЦРЅМК¦±»СЎЦРµДёЕВК.
ДЪµДёГРЈЅМК¦ЦРИОИЎ2ИЛЈ¬ЗуЦБЙЩУР1ГыіхЦРЅМК¦±»СЎЦРµДёЕВК.
Ўѕґр°ёЎїЈЁ1Ј©![]() ИЛ.ЈЁ2Ј©
ИЛ.ЈЁ2Ј©![]()
ЎѕЅвОцЎї
ЈЁ1Ј©ПИЗуµГСщ±ѕЦРіхЦРЎўёЯЦРЅМК¦И±·¦¶НБ¶µДЖµВКЈ¬УЙґЛјЖЛгіцёГРЈЅМК¦ЦРИ±·¦¶НБ¶µДИЛКэ.АыУГБРѕЩ·ЁЈ¬ЅбєП№ЕµдёЕРНёЕВКјЖЛ㹫ʽЈ¬јЖЛгіцЛщЗуёЕВК.
ЈЁ2Ј©АыУГБРѕЩ·ЁЈ¬ЅбєП№ЕµдёЕРНёЕВКјЖЛ㹫ʽЈ¬јЖЛгіцЛщЗуёЕВК.
ЈЁ1Ј©УЙМвТвїЙµГСщ±ѕЦРіхЦРЅМК¦И±·¦¶НБ¶µДЖµВКОЄ![]() Ј¬
Ј¬
Сщ±ѕЦРёЯЦРЅМК¦И±·¦¶НБ¶µДЖµВКОЄ![]() Ј¬
Ј¬
№АјЖёГРЈЅМК¦ЦРИ±·¦¶НБ¶µДИЛКэОЄ![]() .
.
ЈЁ2Ј©УЙМвТвїЙІОУлµчІйіхЦРЅМК¦ГїМмїОНв¶НБ¶К±јдФЪ![]() µДИЛКэОЄ
µДИЛКэОЄ![]() Ј¬јЗОЄ
Ј¬јЗОЄ![]() Ј¬
Ј¬![]() Ј»
Ј»
ёЯЦРЅМК¦ГїМмїОНв¶НБ¶К±јдФЪ![]() µДИЛКэОЄ
µДИЛКэОЄ![]() Ј¬јЗОЄ
Ј¬јЗОЄ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() .
.
ґУХв5ИЛЦРСЎИЎ2ИЛµДЗйїцУР![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬№І10ЦЦЈ»
Ј¬№І10ЦЦЈ»
ЖдЦР·ыєПМхјюµДЗйїцУР![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬№І7ЦЦ.
Ј¬№І7ЦЦ.
№КЛщЗуёЕВК![]() .
.


 МмМмПтЙПТ»±ѕєГѕнПµБРґр°ё
МмМмПтЙПТ»±ѕєГѕнПµБРґр°ё РЎС§Йъ10·ЦЦУУ¦УГМвПµБРґр°ё
РЎС§Йъ10·ЦЦУУ¦УГМвПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЛДАвЧ¶PЎЄABCDЦРЈ¬µЧГжABCDОЄѕШРОЈ¬ЖЅГжPADЎНЖЅГжABCDЈ¬PAPDЈ¬EЈ¬F·Ц±рОЄADЈ¬PBµДЦРµгЈ®ЗуЦ¤Јє
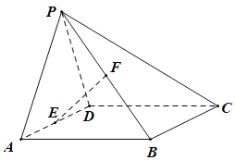
ЈЁ1Ј©EF//ЖЅГжPCDЈ»
ЈЁ2Ј©ЖЅГжPABЖЅГжPCDЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДі№«ЛѕAІъЖ·ЙъІъµДН¶ИліЙ±ѕxЈЁµҐО»ЈєНтФЄЈ©УлІъЖ·ПъКЫКХИлyЈЁµҐО»ЈєК®НтФЄЈ©ґжФЪЅПєГµДПЯРФ№ШПµЈ¬ПВ±нјЗВјБЛёГ№«ЛѕЧоЅь8ґОёГІъЖ·µДПа№ШКэѕЭЈ¬ЗТёщѕЭХв8ЧйКэѕЭјЖЛгµГµЅy№ШУЪxµДПЯРФ»Ш№й·ЅіМОЄ![]() Ј®
Ј®
xЈЁНтФЄЈ© | 6 | 7 | 8 | 11 | 12 | 14 | 17 | 21 |
yЈЁК®НтФЄЈ© | 1.2 | 1.5 | 1.7 | 2 | 2.2 | 2.4 | 2.6 | 2.9 |
ЈЁ1Ј©Зу![]() µДЦµЈЁЅб№ыѕ«И·µЅ0.0001Ј©Ј¬Іў№АјЖ№«ЛѕAІъЖ·Н¶ИліЙ±ѕ30НтФЄєуІъЖ·µДПъКЫКХИлЈЁµҐО»ЈєК®НтФЄЈ©Ј®
µДЦµЈЁЅб№ыѕ«И·µЅ0.0001Ј©Ј¬Іў№АјЖ№«ЛѕAІъЖ·Н¶ИліЙ±ѕ30НтФЄєуІъЖ·µДПъКЫКХИлЈЁµҐО»ЈєК®НтФЄЈ©Ј®
ЈЁ2Ј©ёГ№«ЛѕBІъЖ·ЙъІъµДН¶ИліЙ±ѕuЈЁµҐО»ЈєНтФЄЈ©УлІъЖ·ПъКЫКХИлvЈЁµҐО»ЈєК®НтФЄЈ©ТІґжФЪЅПєГµДПЯРФ№ШПµЈ¬ЗТv№ШУЪuµДПЯРФ»Ш№й·ЅіМОЄ![]() Ј®
Ј®
ЈЁiЈ©№АјЖёГ№«ЛѕBІъЖ·Н¶ИліЙ±ѕ30НтФЄєуµДГ«АыВКЈЁГ«АыВК![]() Ј©Ј»
Ј©Ј»
ЈЁiiЈ©ЕР¶ПёГ№«ЛѕAЈ¬BБЅёцІъЖ·¶јН¶ИліЙ±ѕ30НтФЄєуЈ¬ДДёцІъЖ·µДГ«АыВКёьґуЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
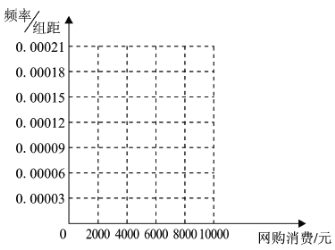
ЎѕМвДїЎїОТ№ъКЗКАЅзЙПСПЦШИ±Л®µД№йјТЦ®Т»Ј¬ДіКРОЄБЛЦЖ¶©єПАнµДЅЪЛ®·Ѕ°ёЈ¬¶ФјТНҐУГЛ®ЗйїцЅшРРБЛійСщµчІйЈ¬»сµГБЛДіДк100ёцјТНҐµДФВѕщУГЛ®БїЈЁµҐО»Јє![]() Ј©µДКэѕЭЈ¬Ѕ«ХвР©КэѕЭ°ґХХ
Ј©µДКэѕЭЈ¬Ѕ«ХвР©КэѕЭ°ґХХ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ·ЦіЙ9ЧйЈ¬ЦЖіЙБЛИзНјЛщКѕµДЖµВК·ЦІјЦ±·ЅНј.
·ЦіЙ9ЧйЈ¬ЦЖіЙБЛИзНјЛщКѕµДЖµВК·ЦІјЦ±·ЅНј.
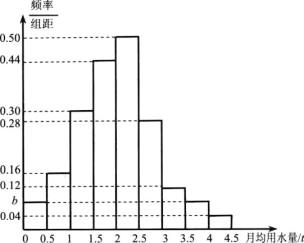
ЈЁ1Ј©ЗуНјЦРµД![]() ЦµЈ¬ИфёГКРУР30НтёцјТНҐЈ¬КФ№АјЖИ«КРФВѕщУГЛ®БїІ»µНУЪ
ЦµЈ¬ИфёГКРУР30НтёцјТНҐЈ¬КФ№АјЖИ«КРФВѕщУГЛ®БїІ»µНУЪ![]() µДјТНҐКэЈ»
µДјТНҐКэЈ»
ЈЁ2Ј©јЩЙиН¬ЧйЦРµДГїёцКэѕЭ¶јУГёГЧйЗшјдµДЦРµгЦµґъМжЈ¬КФ№АјЖИ«КРјТНҐФВѕщУГЛ®БїµДЖЅѕщКэЈ»
ЈЁ3Ј©ПЦґУФВѕщУГЛ®БїФЪ![]() Ј¬
Ј¬![]() µДјТНҐЦРЈ¬ПИ°ґХХ·ЦІгійСщµД·Ѕ·ЁійИЎ9ёцјТНҐЈ¬ФЩґУХв9јТНҐЦРійИЎ4ёцјТНҐЈ¬јЗХв4ёцјТНҐЦРФВѕщУГЛ®БїФЪ
µДјТНҐЦРЈ¬ПИ°ґХХ·ЦІгійСщµД·Ѕ·ЁійИЎ9ёцјТНҐЈ¬ФЩґУХв9јТНҐЦРійИЎ4ёцјТНҐЈ¬јЗХв4ёцјТНҐЦРФВѕщУГЛ®БїФЪ![]() ЦРµДКэБїОЄ
ЦРµДКэБїОЄ![]() Ј¬Зу
Ј¬Зу![]() µД·ЦІјБРј°КэС§ЖЪНы.
µД·ЦІјБРј°КэС§ЖЪНы.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ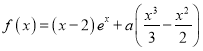 .
.
ЈЁ1Ј©МЦВЫ![]() µДј«ЦµµгµДёцКэЈ»
µДј«ЦµµгµДёцКэЈ»
ЈЁ2Ј©Иф![]() УР3ёцј«Цµµг
УР3ёцј«Цµµг![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ЈЁЖдЦР
ЈЁЖдЦР![]() Ј©Ј¬Ц¤ГчЈє
Ј©Ј¬Ц¤ГчЈє![]() .
.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїОТ№ъРВРН№ЪЧґІЎ¶ѕ·ОСЧТЯЗйЖЪјдЈ¬ТФНшВз№єОпєННшЙП·юОсЛщґъ±нµДРВРЛПы·СХ№ПЦіцБЛЗїґуµДЙъГьБ¦Ј¬РВРЛПы·СЅ«іЙОЄОТ№ъПы·СФці¤µДРВ¶ЇДЬ.ДіКРОЄБЛБЛЅв±ѕµШѕУГсФЪ2020Дк2ФВЦБ3ФВБЅёцФВНшВз№єОпПы·СЗйїцЈ¬ФЪНшЙПЛж»ъ¶Ф1000ИЛЧцБЛОКѕнµчІйЈ¬µГИзПВЖµКэ·ЦІј±нЈє
Нш№єПы·СЗйїцЈЁФЄЈ© |
|
|
|
|
|
ЖµКэ | 300 | 400 | 180 | 60 | 60 |
ЈЁ1Ј©ЧчіцХвР©КэѕЭµДЖµВК·ЦІјЦ±·ЅНјЈ¬Іў№АјЖ±ѕКРѕУГсґЛЖЪјдНшВз№єОпµДПы·СЖЅѕщЦµЈ»
ЈЁ2Ј©ФЪµчІйОКѕнЦРУРТ»ПоКЗМоРґ±ѕИЛДкБдЈ¬ОЄСРѕїНш№єЅр¶оєННш№єИЛДкБдµД№ШПµЈ¬ТФНш№єЅр¶оКЗ·сі¬№э4000ФЄОЄ±кЧјЅшРР·ЦІгійСщЈ¬ґУЙПКц1000ИЛЦРійИЎ200ИЛЈ¬µГµЅИзПВБРБЄ±нЈ¬ЗлЅ«±нІ№ідНкХыІўёщѕЭБРБЄ±нЕР¶ПЈ¬ФЪґЛЖЪјдКЗ·сУР95%µД°СОХИПОЄНш№єЅр¶оУлНш№єИЛДкБдУР№Ш.
Нш№єІ»і¬№э4000ФЄ | Нш№єі¬№э4000ФЄ | ЧЬјЖ | |
40ЛкТФЙП | 75 | 100 | |
40ЛкТФПВЈЁє¬40ЛкЈ© | |||
ЧЬјЖ | 200 |
ІОїј№«КЅєНКэѕЭЈє![]() .ЈЁЖдЦР
.ЈЁЖдЦР![]() ОЄСщ±ѕИЭБїЈ©
ОЄСщ±ѕИЭБїЈ©
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() ФтxЎК[©Ѓ1Ј¬e]К±Ј¬fЈЁxЈ©µДЧоРЎЦµОЄ_____Ј»ЙиgЈЁxЈ©ЈЅ[fЈЁxЈ©]2©ЃfЈЁxЈ©+aИфєЇКэgЈЁxЈ©УР6ёцБгµгЈ¬ФтКµКэaµДИЎЦµ·¶О§КЗ_____Ј®
ФтxЎК[©Ѓ1Ј¬e]К±Ј¬fЈЁxЈ©µДЧоРЎЦµОЄ_____Ј»ЙиgЈЁxЈ©ЈЅ[fЈЁxЈ©]2©ЃfЈЁxЈ©+aИфєЇКэgЈЁxЈ©УР6ёцБгµгЈ¬ФтКµКэaµДИЎЦµ·¶О§КЗ_____Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЦ±ЅЗЧш±кПµ![]() ЦРЈ¬ЗъПЯ
ЦРЈ¬ЗъПЯ![]() Ј¬ЗъПЯ
Ј¬ЗъПЯ![]() ЈЁ
ЈЁ![]() ОЄІОКэЈ©Ј¬ТФЧш±кФµг
ОЄІОКэЈ©Ј¬ТФЧш±кФµг![]() ОЄј«µгЈ¬ТФ
ОЄј«µгЈ¬ТФ![]() ЦбµДХэ°лЦбОЄј«ЦбЅЁБўј«Чш±кПµ.
ЦбµДХэ°лЦбОЄј«ЦбЅЁБўј«Чш±кПµ.
ЈЁ1Ј©Зу![]() µДј«Чш±к·ЅіМЈ»
µДј«Чш±к·ЅіМЈ»
ЈЁ2Ј©ЙдПЯ![]() µДј«Чш±к·ЅіМОЄ
µДј«Чш±к·ЅіМОЄ![]() Ј¬Иф
Ј¬Иф![]() ·Ц±рУл
·Ц±рУл![]() Ѕ»УЪТмУЪј«µгµД
Ѕ»УЪТмУЪј«µгµД![]() БЅµгЈ¬Зу
БЅµгЈ¬Зу![]() µДЧоґуЦµ.
µДЧоґуЦµ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЛ«ЗъПЯ![]() µДРйЦбµДТ»ёц¶ҐµгОЄ
µДРйЦбµДТ»ёц¶ҐµгОЄ![]() Ј¬Ч󶥵гОЄ
Ј¬Ч󶥵гОЄ![]() Ј¬Л«ЗъПЯ
Ј¬Л«ЗъПЯ![]() µДЧуЎўУТЅ№µг·Ц±рОЄ
µДЧуЎўУТЅ№µг·Ц±рОЄ![]() Ј¬
Ј¬![]() Ј¬µг
Ј¬µг![]() ОЄПЯ¶О
ОЄПЯ¶О![]() ЙПµД¶ЇµгЈ¬µ±
ЙПµД¶ЇµгЈ¬µ±![]() ИЎµГЧоРЎЦµєНЧоґуЦµК±Ј¬
ИЎµГЧоРЎЦµєНЧоґуЦµК±Ј¬![]() µДГж»э·Ц±рОЄ
µДГж»э·Ц±рОЄ![]() Ј¬
Ј¬![]() Ј¬Иф
Ј¬Иф![]() Ј¬ФтЛ«ЗъПЯ
Ј¬ФтЛ«ЗъПЯ![]() µДАлРДВКОЄЈЁ Ј©Ј®
µДАлРДВКОЄЈЁ Ј©Ј®
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com