
| 条件 | 方程 | ||||
| ①△ABC周长为10; ②△ABC面积为10; ③△ABC中,∠A=90° |
E1:y2=25; E2:x2+y2=4(y≠0); E3:
|
| 1 |
| 2 |
| AB |
| AC |


科目:高中数学 来源: 题型:013
下面是一道选择题的两种解法,两种解法看似都对,可结果并不一致,问题出在哪里
?在△ABC中,a=x,b=2,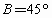 ,若△ABC有两解,则x的取值范围是
,若△ABC有两解,则x的取值范围是
[
]|
A .(2,+∞) |
B .(0,2) |
C .(2,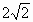 ) ) |
D .(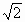 ,2) ,2) |
解法
1 △ABC有两解,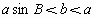 ,
,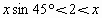 ,
,
即
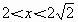 ,故选C.
,故选C.
解法
2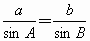 ,
,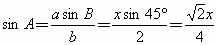 .
.
△
ABC有两解,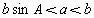 ,
,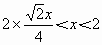 ,即0<x<2,故选B.
,即0<x<2,故选B.查看答案和解析>>
科目:高中数学 来源:山西省山大附中2011-2012学年高一5月月考数学试题(A) 题型:022
在△ABC中,a=x,b=2,B=45°,若三角形有两解,则x的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省台州市玉环县玉城中学高二(上)第二次月考数学试卷(解析版) 题型:选择题
| 条件 | 方程 |
| ①△ABC周长为10; ②△ABC面积为10; ③△ABC中,∠A=90° | E1:y2=25; E2:x2+y2=4(y≠0); E3: 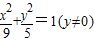 |
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,a=x,b=2,B=45°,若这样的△ABC有两个,则实数x的取值范围是( )
A.(2,+∞) B.(0,2) C.(2,2![]() ) D.(
) D.(![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com