
【题目】孔子曰:温故而知新.数学学科的学习也是如此.为了调查数学成绩与及时复习之间的关系,某校志愿者展开了积极的调查活动:从高三年级640名学生中按系统抽样抽取40名学生进行问卷调查,所得信息如下:
数学成绩优秀(人数) | 数学成绩合格(人数) | |
及时复习(人数) | 20 | 4 |
不及时复习(人数) | 10 | 6 |
(1)张军是640名学生中的一名,他被抽中进行问卷调查的概率是多少(用分数作答);
(2)根据以上数据,运用独立性检验的基本思想,研究数学成绩与及时复习的相关性.
参考公式: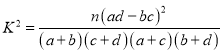 ,其中
,其中![]() 为样本容量
为样本容量
临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
科目:高中数学 来源: 题型:
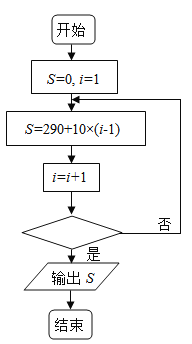
【题目】《九章算术》中盈不足章中有这样一则故事:“今有良马与驽马发长安,至齐. 齐去长安三千里. 良马初日行一百九十三里,日增一十二里;驽马初日行九十七里,日减二里.” 为了计算每天良马和驽马所走的路程之和,设计框图如下图. 若输出的 ![]() 的值为 350,则判断框中可填( )
的值为 350,则判断框中可填( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有下列四个命题:
p1:两两相交且不过同一点的三条直线必在同一平面内.
p2:过空间中任意三点有且仅有一个平面.
p3:若空间两条直线不相交,则这两条直线平行.
p4:若直线l![]() 平面α,直线m⊥平面α,则m⊥l.
平面α,直线m⊥平面α,则m⊥l.
则下述命题中所有真命题的序号是__________.
①![]() ②
②![]() ③
③![]() ④
④![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大报告要求,确保到2020年我国现行标准下农村贫困人口实现脱贫,贫困县全部摘帽,解决区域性整体贫困,做到脱真贫、真脱贫.某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领农村地区人民群众脱贫奔小康,扶贫办计划为某农村地区购买农机机器,假设该种机器使用三年后即被淘汰.农机机器制造商对购买该机器的客户推出了两种销售方案:
方案一:每台机器售价7000元,三年内可免费保养2次,超过2次每次收取保养费200元;
方案二:每台机器售价7050元,三年内可免费保养3次,超过3次每次收取保养费100元.
扶贫办需要决策在购买机器时应该选取那种方案,为此搜集并整理了50台这种机器在三年使用期内保养的次数,得下表:
保养次数 | 0 | 1 | 2 | 3 | 4 | 5 |
台数 | 1 | 10 | 19 | 14 | 4 | 2 |
记x表示1台机器在三年使用期内的保养次数.
(1)用样本估计总体的思想,求“x不超过3”的概率;
(2)按照两种销售方案,分别计算这50台机器三年使用期内的总费用(总费用=售价+保养费),以每台每年的平均费用作为决策依据,扶贫办选择那种销售方案购买机器更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义在
是定义在![]() 上的函数,满足
上的函数,满足![]() ,且对任意的
,且对任意的![]() ,恒有
,恒有![]() ,已知当
,已知当![]() 时,
时,![]() ,则有( )
,则有( )
A.函数![]() 的最大值是1,最小值是
的最大值是1,最小值是![]()
B.函数![]() 是周期函数,且周期为2
是周期函数,且周期为2
C.函数![]() 在
在![]() 上递减,在
上递减,在![]() 上递增
上递增
D.当![]() 时,
时,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),![]() ,
,![]() 为曲线
为曲线![]() 上的一动点.
上的一动点.
(I)求动点![]() 对应的参数从
对应的参数从![]() 变动到
变动到![]() 时,线段
时,线段![]() 所扫过的图形面积;
所扫过的图形面积;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 的另一个交点为
的另一个交点为![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 为线段
为线段![]() 的中点?若存在,求出点
的中点?若存在,求出点![]() 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com