
【题目】已知函数![]() 的图象与x轴交点为
的图象与x轴交点为![]() ,与此交点距离最小的最高点坐标为
,与此交点距离最小的最高点坐标为![]() .
.
(Ⅰ)求函数![]() 的表达式;
的表达式;
(Ⅱ)若函数![]() 满足方程
满足方程![]() ,求方程在
,求方程在![]() 内的所有实数根之和;
内的所有实数根之和;
(Ⅲ)把函数![]() 的图像的周期扩大为原来的两倍,然后向右平移
的图像的周期扩大为原来的两倍,然后向右平移![]() 个单位,再把纵坐标伸长为原来的两倍,最后向上平移一个单位得到函数
个单位,再把纵坐标伸长为原来的两倍,最后向上平移一个单位得到函数![]() 的图像.若对任意的
的图像.若对任意的![]() ,方程
,方程![]() 在区间
在区间![]() 上至多有一个解,求正数k的取值范围.
上至多有一个解,求正数k的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
(Ⅰ)依题意作出部分函数图像,由最大值确定A,周期确定![]() ,特殊点
,特殊点![]() 确定
确定![]() 即可求出解析式;(Ⅱ)由周期知
即可求出解析式;(Ⅱ)由周期知![]() 在
在![]() 内恰有2个周期,则方程有四个根,结合图像利用对称轴即可求出所有根的和;(Ⅲ)根据三角函数的图像变化,数形结合即可得到结论.
内恰有2个周期,则方程有四个根,结合图像利用对称轴即可求出所有根的和;(Ⅲ)根据三角函数的图像变化,数形结合即可得到结论.
(Ⅰ)从图知,函数的最大值为1,则![]() ,
,

函数![]() 的周期为
的周期为![]() ,而
,而![]() ,则
,则![]()
又![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
解得![]() ,而
,而![]() ,则
,则![]() ,
,
∴函数![]() 的表达式为
的表达式为![]() .
.
(Ⅱ)![]() 的周期为
的周期为![]() ,
,
![]() 在
在![]() 内恰有2个周期,
内恰有2个周期,
并且方程![]() 在
在![]() 内有4个实根设为
内有4个实根设为![]() ,
,
结合图像知![]() .
.
故所有实数之和为![]() .
.
(Ⅲ)先把![]() 的图像的周期扩大为原来的两倍,得到
的图像的周期扩大为原来的两倍,得到![]() ,然后向右平移
,然后向右平移![]() 个单位得到
个单位得到![]() ,纵坐标伸长为原来的2倍再向上平移1个单位得到
,纵坐标伸长为原来的2倍再向上平移1个单位得到![]() ,
,
函数![]() 的图象如图所示,
的图象如图所示,
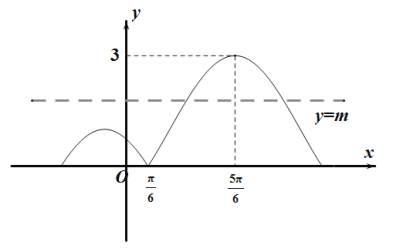
则当![]() 图象伸长为原来的5倍以上时符合题意,所以
图象伸长为原来的5倍以上时符合题意,所以![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 上,
上,![]() 平面
平面![]() ,
,![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
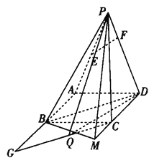
(1)证明:![]() 平面
平面![]() .
.
(2)过点![]() 作
作![]() 的平行线,与直线
的平行线,与直线![]() 相交于点
相交于点![]() ,点
,点![]() 为
为![]() 的中点,求
的中点,求![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为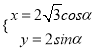 ,其中
,其中![]() 为参数,在以坐标原点
为参数,在以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() , 直线
, 直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点, ![]() 为线段
为线段![]() 的中点.求点
的中点.求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】幻彩摩天轮位于中山市西区兴中广场C段4层高的建筑之上,与中山市第一家四星级酒店——富华酒店隔河相望,其外观是参考世界最高的摩天轮新加坡“飞行者”的设计,轮体上有36个吊舱,共可同时承载288人从高空俯瞰岐江一河两岸的美景.幻彩摩天轮直径为83m,每20min转一圈,最高点离地108m,摩天轮上的点P的起始位置在最低点处.已知在时刻t(min)时P距离地面的高度![]() ,(其中
,(其中![]() ),
),
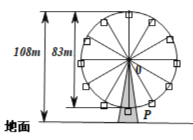
(1)求![]() 的函数解析式.
的函数解析式.
(2)当离地面![]() m以上时,可以俯瞰富华酒店顶楼,求转一圈中有多少时间可以俯瞰富华酒店顶楼?
m以上时,可以俯瞰富华酒店顶楼,求转一圈中有多少时间可以俯瞰富华酒店顶楼?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )的部分图象如图所示.
)的部分图象如图所示.
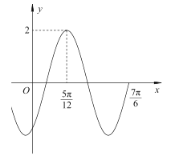
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的最小值及
的最小值及![]() 取到最小值时自变量x的集合;
取到最小值时自变量x的集合;
(3)将函数图像上所有点的纵坐标不变,横坐标变为原来的![]() (
(![]() )倍,得到函数
)倍,得到函数![]() 的图象.若函数
的图象.若函数![]() 在区间
在区间![]() 上恰有5个零点,求t的取值范围.
上恰有5个零点,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知△![]() 中,∠
中,∠![]() =90°,
=90°,![]() ,且
,且![]() =1,
=1,![]() =2,△
=2,△![]() 绕
绕![]() 旋转至
旋转至![]() ,使点
,使点![]() 与点
与点![]() 之间的距离
之间的距离![]() =
=![]() .
.
(1)求证:![]() ⊥平面
⊥平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求异面直线![]() 与
与![]() 所成的角的余弦值.
所成的角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不交于同一点的三条直线![]() :4x+y-4=0,
:4x+y-4=0,![]() :mx+y=0,
:mx+y=0,![]() :x-my-4=0.
:x-my-4=0.
(1)当这三条直线不能围成三角形时,求实数m的值;
(2)当![]() 与
与![]() ,
,![]() 都垂直时,求两垂足间的距离.
都垂直时,求两垂足间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com