
【题目】如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ. 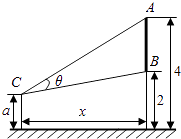
(1)若a=1.5,问:观察者离墙多远时,视角θ最大?
(2)若tanθ= ![]() ,当a变化时,求x的取值范围.
,当a变化时,求x的取值范围.
【答案】
(1)解:如图,作CD⊥AF于D,则CD=EF,
设∠ACD=α,∠BCD=β,CD=x,则θ=α﹣β,
在Rt△ACD和Rt△BCD中,tanα= ![]() ,tanβ=
,tanβ= ![]() ,
,
则tanθ=tan(α﹣β)= ![]() =
= ![]() (x>0),
(x>0),
令u= ![]() ,则ux2﹣2x+1.25u=0,
,则ux2﹣2x+1.25u=0,
∵上述方程有大于0的实数根,∴△≥0,
即4﹣4×1.25u2≥0,∴u≤ ![]() ,即(tanθ)max=
,即(tanθ)max= ![]() ,
,
∵正切函数y=tanx在(0, ![]() )上是增函数,
)上是增函数,
∴视角θ同时取得最大值,
此时,x= ![]() =
= ![]() ,
,
∴观察者离墙 ![]() 米远时,视角θ最大
米远时,视角θ最大

(2)解:由(1)可知,tanθ= ![]() =
= 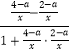 =
= ![]() ,
,
即x2﹣4x+4=﹣a2+6a﹣4,
∴(x﹣2)2=﹣(a﹣3)2+5,
∵1≤a≤2,
∴1≤(x﹣2)2≤4,
化简得:0≤x≤1或3≤x≤4,
又∵x>1,
∴3≤x≤4.
【解析】(1)首项利用两角和的正切公式建立函数关系,进一步利用判别式确定函数的最大值;(2)利用两角和的正切公式建立函数关系,利用a的取值范围即可确定x的范围.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线![]() 上的点
上的点 对应的参数
对应的参数![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若点![]() ,
, ![]() 在曲线
在曲线![]() 上,求
上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们国家正处于老龄化阶段,“老有所依”也是政府的民生工程.为了了解老人们的健康状况,政府从老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行统计,样本分布被制作成如图表.

(1)若采用分层抽样的方法,再从样本中不能自理的老人中抽取16人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)据统计该市大约有![]() 的户籍老人无固定收入,且在各健康状况人群中所占比例相同,政府计划每月为这部分老人发放生活补贴,标准如下:
的户籍老人无固定收入,且在各健康状况人群中所占比例相同,政府计划每月为这部分老人发放生活补贴,标准如下:
①80岁及以上长者每人每月发放生活补贴200元;
②80岁以下老人每人每月发放生活补贴120元;
③不能自理的老人每人每月额外再发放生活补贴100元.
若用频率估计概率,设任意户籍老人每月享受的生活补贴为![]() 元,求
元,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在高三抽取了500名学生,记录了他们选修A、B、C三门课的选修情况,如表:
科目 学生人数 | A | B | C |
120 | 是 | 否 | 是 |
60 | 否 | 否 | 是 |
70 | 是 | 是 | 否 |
50 | 是 | 是 | 是 |
150 | 否 | 是 | 是 |
50 | 是 | 否 | 否 |
(Ⅰ)试估计该校高三学生在A、B、C三门选修课中同时选修2门课的概率.
(Ⅱ)若该高三某学生已选修A,则该学生同时选修B、C中哪门的可能性大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列向量组中,可以把向量 ![]() =(3,2)表示出来的是( )
=(3,2)表示出来的是( )
A.![]() =(0,0),
=(0,0), ![]() =(1,2)
=(1,2)
B.![]() =(﹣1,2),
=(﹣1,2), ![]() =(5,﹣2)
=(5,﹣2)
C.![]() =(3,5),
=(3,5), ![]() =(6,10)
=(6,10)
D.![]() =(2,﹣3),
=(2,﹣3), ![]() =(﹣2,3)
=(﹣2,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
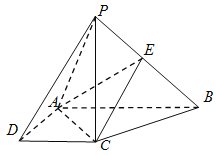
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的点.
上的点.
(Ⅰ)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)若![]() 是
是![]() 的中点,且二面角
的中点,且二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com