
【题目】设函数f(x)=|x+m|.
(Ⅰ) 解关于m的不等式f(1)+f(﹣2)≥5;
(Ⅱ)当x≠0时,证明: ![]() .
.
科目:高中数学 来源: 题型:
【题目】手机支付也称为移动支付![]() ,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.
,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.
组数 | 第l组 | 第2组 | 第3组 | 第4组 | 第5组 |
分组 |
|
|
|
|
|
频数 | 20 | 36 | 30 | 10 | 4 |

(1)求![]() ;
;
(2)从第l,3,4组中用分层抽样的方法抽取6人,求第l,3,4组抽取的人数:
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体![]() 中,侧面对角线
中,侧面对角线![]() ,
,![]() 上分别有一点E,F,且
上分别有一点E,F,且![]() ,则直线EF与平面ABCD所成的角的大小为( )
,则直线EF与平面ABCD所成的角的大小为( )

A.0°B.60°C.45°D.30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年春季,世界各地相继出现流感疫情,这已经成为全球性的公共卫生问题.为了考察某种流感疫苗的效果,某实验室随机抽取100只健康小鼠进行试验,得到如下列联表:
感染 | 未感染 | 总计 | |
注射 | 10 | 40 | 50 |
未注射 | 20 | 30 | 50 |
总计 | 30 | 70 | 100 |
参照附表,在犯错误的概率最多不超过__________的前提下,可认为“注射疫苗”与“感染流感”有关系.
(参考公式:![]() .)
.)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个人下半身长(肚脐至足底)与全身长的比近似为![]() (
(![]() ,称为黄金分割比),堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好,若某人着装前测得头顶至肚脐长度为72
,称为黄金分割比),堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好,若某人着装前测得头顶至肚脐长度为72![]() ,肚脐至足底长度为103
,肚脐至足底长度为103![]() ,根据以上数据,作为形象设计师的你,对TA的着装建议是( )
,根据以上数据,作为形象设计师的你,对TA的着装建议是( )
A.身材完美,无需改善B.可以戴一顶合适高度的帽子
C.可以穿一双合适高度的增高鞋D.同时穿戴同样高度的增高鞋与帽子
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知海岛![]() 在海岛
在海岛![]() 北偏东
北偏东![]() ,
,![]() ,
,![]() 相距
相距![]() 海里,物体甲从海岛
海里,物体甲从海岛![]() 以
以![]() 海里/小时的速度沿直线向海岛
海里/小时的速度沿直线向海岛![]() 移动,同时物体乙从海岛
移动,同时物体乙从海岛![]() 沿着海岛
沿着海岛![]() 北偏西
北偏西![]() 方向以
方向以![]() 海里/小时的速度移动.
海里/小时的速度移动.
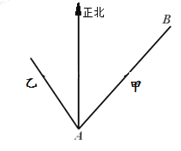
(1)问经过多长时间,物体甲在物体乙的正东方向;
(2)求甲从海岛![]() 到达海岛
到达海岛![]() 的过程中,甲、乙两物体的最短距离.
的过程中,甲、乙两物体的最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 与
与![]() 有表格中的数据,且
有表格中的数据,且![]() 与
与![]() 线性相关,由最小二乘法得
线性相关,由最小二乘法得![]() .
.
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)求![]() 与
与![]() 的线性回归方程;
的线性回归方程;
(2)现有第二个线性模型:![]() ,且
,且![]() .若与(1)的线性模型比较,哪一个线性模型拟合效果比较好,请说明理由
.若与(1)的线性模型比较,哪一个线性模型拟合效果比较好,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com