
【题目】现有2位男生,3位女生去参加一个联欢活动,该活动有甲、乙两个项目可供参加者选择.
(Ⅰ)为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个项目联欢,掷出点数为1或2的人去参加甲项目联欢,掷出点数大于2的人去参加乙项目联欢.求这5人中恰好有3人去参加甲项目联欢的概率;
(Ⅱ)若从这5人中随机选派3人去参加甲项目联欢,设![]() 表示这3个人中女生的人数,求随机变量
表示这3个人中女生的人数,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣alnx,a>0.
(1)若f(x)在x=1处取得极值,求实数a的值;
(2)求f(x)在区间[2,+∞)上的最小值;
(3)在(1)的条件下,若g(x)=x2﹣f(x),求证:当1<x<e2,恒有x![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(m﹣1)x2+3x﹣2m,(m∈R).
(1)解关于x的不等式f(x)+x2﹣1<4x﹣m;
(2)若f(x)<0的解集为(﹣4,1),g(x)=f(x)﹣x+5,对于n∈N*,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
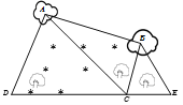
【题目】如图,为了测量某湿地![]() 两点间的距离,观察者找到在同一直线上的三点
两点间的距离,观察者找到在同一直线上的三点![]() .从
.从![]() 点测得
点测得![]() ,从
,从![]() 点测得
点测得![]() ,
,![]() ,从
,从![]() 点测得
点测得![]() .若测得
.若测得![]() ,
,![]() (单位:百米),则
(单位:百米),则![]() 两点的距离为( )
两点的距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ),若点
),若点![]() 是函数
是函数![]() 图象的一个对称中心.
图象的一个对称中心.
(1)求![]() 的解析式,并求
的解析式,并求![]() 的最小正周期;
的最小正周期;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再将所得图象上各点的横坐标伸长为原来的
个单位,再将所得图象上各点的横坐标伸长为原来的![]() 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数![]() 的图象,用 “五点作图法”作出函数
的图象,用 “五点作图法”作出函数![]() 在区间
在区间![]() 上的图象.
上的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面真角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为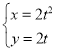 (t为参数),以原点O为极点,x轴正半轴为极轴,建立根坐标系.曲线
(t为参数),以原点O为极点,x轴正半轴为极轴,建立根坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与曲线
与曲线![]() 交于M,N两点,直线OM和ON的斜率分别为
交于M,N两点,直线OM和ON的斜率分别为![]() 和
和![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义![]() 为不超过
为不超过![]() 的最大整数,例如
的最大整数,例如![]() ,
,![]() .已知
.已知![]() 是等比数列,若
是等比数列,若![]() ,且前
,且前![]() 项和为
项和为![]() .
.
(1)若不等式![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)求![]() 的通项公式;
的通项公式;
(3)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,判断是否存在以原点
有且仅有一个公共点,判断是否存在以原点![]() 为圆心的圆,满足此圆与
为圆心的圆,满足此圆与![]() 相交两点
相交两点![]() ,
,![]() (两点均不在坐标轴上),且使得直线
(两点均不在坐标轴上),且使得直线![]() ,
,![]() 的斜率之积为定值?若存在,求此圆的方程与定值;若不存在,请说明理由.
的斜率之积为定值?若存在,求此圆的方程与定值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com