
【题目】已知函数![]() ,直线
,直线![]() :
:![]() .
.
(Ⅰ)设![]() 是
是![]() 图象上一点,
图象上一点,![]() 为原点,直线
为原点,直线![]() 的斜率
的斜率![]() ,若
,若![]() 在
在![]()
![]() 上存在极值,求
上存在极值,求![]() 的取值范围;
的取值范围;
(Ⅱ)是否存在实数![]() ,使得直线
,使得直线![]() 是曲线
是曲线![]() 的切线?若存在,求出
的切线?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(Ⅲ)试确定曲线![]() 与直线
与直线![]() 的交点个数,并说明理由.
的交点个数,并说明理由.
【答案】![]() ,(Ⅲ)见解析
,(Ⅲ)见解析
【解析】
(Ⅰ)先根据斜率公式列![]() 再求导数及其零点,最后根据条件列不等式,解得结果,(Ⅱ)设切点,根据导数几何意义得斜率,再根据点斜式得切线方程,最后根据切线过(0,-1)点列方程,解得切点坐标,即得
再求导数及其零点,最后根据条件列不等式,解得结果,(Ⅱ)设切点,根据导数几何意义得斜率,再根据点斜式得切线方程,最后根据切线过(0,-1)点列方程,解得切点坐标,即得![]() 的值;(Ⅲ)先变量分离,转化为研究函数
的值;(Ⅲ)先变量分离,转化为研究函数![]() 图象,利用导数研究其单调性,再结合函数图象确定交点个数.
图象,利用导数研究其单调性,再结合函数图象确定交点个数.
(Ⅰ)∵![]() ,∴
,∴![]() ,解得
,解得![]() .
.
由题意得: ![]() ,解得
,解得![]() .
.
(Ⅱ)假设存在实数![]() ,使得直线是曲线
,使得直线是曲线![]() 的切线,令切点
的切线,令切点![]() ,
,
∴切线的斜率![]() .
.
∴切线的方程为![]() ,
,
又∵切线过(0,-1)点,
∴![]() .
.
解得![]() ,∴
,∴![]() ,
,
∴![]() .
.
(Ⅲ)由题意,令![]() , 得
, 得 ![]() .
.
令![]() , ∴
, ∴![]() ,由
,由![]() ,解得
,解得![]() .
.
∴![]() 在(0,1)上单调递增,在
在(0,1)上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() ,又
,又![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
![]() 时,只有一个交点;
时,只有一个交点;![]() 时,有两个交点;
时,有两个交点;
![]() 时,没有交点.
时,没有交点.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
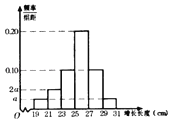
【题目】为了解某养殖产品在某段时间内的生长情况,在该批产品中随机抽取了120件样本,测量其增长长度(单位:![]() ),经统计其增长长度均在区间
),经统计其增长长度均在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,制成频率分布直方图,如图所示其中增长长度为
分成6组,制成频率分布直方图,如图所示其中增长长度为![]() 及以上的产品为优质产品.
及以上的产品为优质产品.
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)已知这120件产品来自于![]() ,
,![]() 两个试验区,部分数据如下列联表:
两个试验区,部分数据如下列联表:
|
| 合计 | |
优质产品 | 20 | ||
非优质产品 | 60 | ||
合计 |
将联表补充完整,并判断是否有![]() 的把握认为优质产品与
的把握认为优质产品与![]() ,
,![]() 两个试验区有关系,并说明理由;
两个试验区有关系,并说明理由;
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
(Ⅲ)以样本的频率代表产品的概率,从这批产品中随机抽取4件进行分析研究,计算抽取的这4件产品中含优质产品的件数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,长半轴长与短半轴长的比值为
,长半轴长与短半轴长的比值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .若点
.若点![]() 在以线段
在以线段![]() 为直径的圆上,求直线
为直径的圆上,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的右焦点为F(2,0),过点F的直线交椭圆于M、N两点且MN的中点坐标为
的右焦点为F(2,0),过点F的直线交椭圆于M、N两点且MN的中点坐标为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l不经过点P(0,b)且与C相交于A,B两点,若直线PA与直线PB的斜率的和为1,试判断直线 l是否经过定点,若经过定点,请求出该定点;若不经过定点,请给出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年全国“两会”,即中华人民共和国第十三届全国人大二次会议和中国人民政治协商会议第十三届全国委员会第二次会议,分别于2019年3月5日和3月3日在北京召开.为了了解哪些人更关注“两会”,某机构随机抽取了年龄在15~75岁之间的200人进行调查,并按年龄绘制的频率分布直方图如下图所示,把年龄落在区间[15,35)和[35,75]内的人分别称为“青少年人”和“中老年人”.经统计“青少年人”和“中老年人”的人数之比为19:21.其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是2:1.
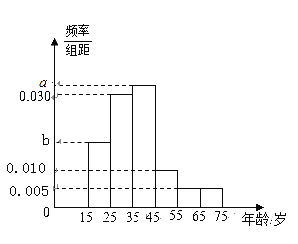
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)现采用分层抽样在[25,35)和[45,55)中随机抽取8名代表,从8人中任选2人,求2人中至少有1个是“中老年人”的概率是多少?
(Ⅲ)根据已知条件,完成下面的2×2列联表,并根据此统计结果判断:能否有99.9%的把握认为“中老年人”比“青少年人”更加关注“两会”?
关注 | 不关注 | 合计 | |
青少年人 | |||
中老年人 | |||
合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“水是生命之源”,但是据科学界统计可用淡水资源仅占地球储水总量的![]() ,全世界近
,全世界近![]() 人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准
人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨):一位居民的月用水量不超过
(吨):一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(1)求直方图中![]() 的值;
的值;
(2)设该市有60万居民,估计全市居民中月均用水量不低于2.5吨的人数,并说明理由;
(3)若该市政府希望使![]() 的居民每月的用水不按议价收费,估计
的居民每月的用水不按议价收费,估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com