
【题目】设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(﹣3)=0,则不等式f(x)g(x)<0的解集是( )
A.(﹣3,0)∪(3,+∞)
B.(﹣3,0)∪(0,3)
C.(﹣∞,﹣3)∪(3,+∞)
D.(﹣∞,﹣3)∪(0,3)
【答案】D
【解析】解:设F(x)=f (x)g(x),当x<0时,
∵F′(x)=f′(x)g(x)+f (x)g′(x)>0.
∴F(x)在当x<0时为增函数.
∵F(﹣x)=f (﹣x)g (﹣x)=﹣f (x)g (x)=﹣F(x).
故F(x)为(﹣∞,0)∪(0,+∞)上的奇函数.
∴F(x)在(0,+∞)上亦为增函数.
已知g(﹣3)=0,必有F(﹣3)=F(3)=0.
构造如图的F(x)的图象,可知
F(x)<0的解集为x∈(﹣∞,﹣3)∪(0,3).
故选D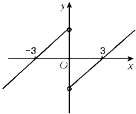
先根据f’(x)g(x)+f(x)g’(x)>0可确定[f(x)g(x)]'>0,进而可得到f(x)g(x)在x<0时递增,结合函数f(x)与g(x)的奇偶性可确定f(x)g(x)在x>0时也是增函数,最后根据g(﹣3)=0可求得答案.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
【题目】设曲线y=xn+1(n∈N*)在点(1,1)处的切线与x轴的交点的横坐标为xn , 令an=lgxn , 则a1+a2+…+a99的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了培养学生的数学建模和应用能力,某校组织了一次实地测量活动,如图,假设待测量的树木AE的高度H(m),垂直放置的标杆BC的高度h=4m,仰角∠ABE=α,∠ADE=β(D,C,E三点共线),试根据上述测量方案,回答如下问题: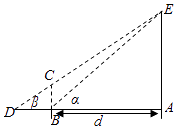
(1)若测得α=60°、β=30°,试求H的值;
(2)经过分析若干次测得的数据后,大家一致认为适当调整标杆到树木的距离d(单位:m),使α与β之差较大时,可以提高测量精确度.
若树木的实际高度为8m,试问d为多少时,α﹣β最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,过焦点垂直长轴的弦长为3.
,过焦点垂直长轴的弦长为3.
(1)求椭圆的标准方程;
(2)过椭圆的右顶点作直线交抛物线y2=2x于A、B两点,求证:OA⊥OB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知正方体ABCD-A1B1C1D1.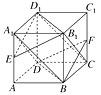
(1)求证:平面A1BD∥平面B1D1C.
(2)若E , F分别是AA1 , CC1的中点,求证:平面EB1D1∥平面FBD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设(x1 , y1),(x2 , y2),…,(xn , yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是( ) 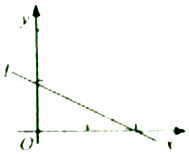
A.x和y的相关系数在﹣1和0之间
B.x和y的相关系数为直线l的斜率
C.当n为偶数时,分布在l两侧的样本点的个数一定相同
D.所有样本点(xi , yi)(i=1,2,…,n)都在直线l上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知sinB+sinA(sinC﹣cosC)=0,a=2,c= ![]() ,则C=( )
,则C=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com