
 种取法,再从余下的五本书中任取两本,作为两本一堆,有C
种取法,再从余下的五本书中任取两本,作为两本一堆,有C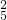 种取法,再后从余下三本取三本作为一堆,有C
种取法,再后从余下三本取三本作为一堆,有C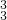 种取法,故共有分法C
种取法,故共有分法C C
C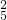 C
C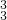 =60种.…(3分)
=60种.…(3分) C
C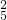 C
C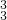 种,第每种分组方法仅对应一种分配方法,
种,第每种分组方法仅对应一种分配方法, C
C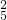 C
C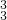 =60种.
=60种. C
C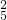 C
C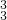 种,但每种分组方法又有A
种,但每种分组方法又有A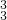 种分配方法,
种分配方法, C
C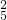 C
C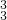 A
A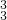 =360种.
=360种.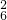 种,甲不论用哪一种方法取得2本书后,已再从余下的4本书中取书有C
种,甲不论用哪一种方法取得2本书后,已再从余下的4本书中取书有C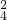 种方法,而甲、乙不论用哪一种方法各取2本书后,丙从余下的两本中取两本书,有C
种方法,而甲、乙不论用哪一种方法各取2本书后,丙从余下的两本中取两本书,有C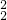 种方法,
种方法,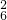 C
C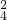 C
C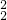 =90种方法.…(12分)
=90种方法.…(12分)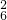 C
C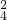 C
C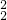 ÷A
÷A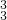 =15种分堆方法.
=15种分堆方法. 种取法,再从余下的五本书中任取两本,作为两本一堆,有C
种取法,再从余下的五本书中任取两本,作为两本一堆,有C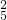 种取法,再后从余下三本取三本作为一堆,有C
种取法,再后从余下三本取三本作为一堆,有C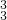 种取法,最后根据乘法得出共有分法C
种取法,最后根据乘法得出共有分法C C
C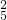 C
C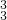 种方法;
种方法; C
C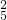 C
C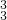 种,但每种分组方法又有A
种,但每种分组方法又有A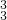 种分配方法,根据乘法原理得出一人得一本,一人得二本,一人得三本的分法种数即可;
种分配方法,根据乘法原理得出一人得一本,一人得二本,一人得三本的分法种数即可;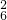 种,甲不论用哪一种方法取得2本书后,已再从余下的4本书中取书有C
种,甲不论用哪一种方法取得2本书后,已再从余下的4本书中取书有C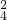 种方法,而甲、乙不论用哪一种方法各取2本书后,丙从余下的两本中取两本书,有C
种方法,而甲、乙不论用哪一种方法各取2本书后,丙从余下的两本中取两本书,有C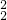 种方法,所以一共有C
种方法,所以一共有C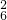 C
C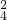 C
C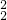 种方法;
种方法;

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)一堆一本,一堆两本,一堆三本;
(2)甲得一本,乙得两本,丙得三本;
(3)一人得一本,一人得两本,一人得三本;
(4)平均分给甲、乙、丙三人;
(5)平均分成三堆.
查看答案和解析>>
科目:高中数学 来源: 题型:
6本不同的书,按照以下要求处理,各有几种分法?
(1)一堆一本,一堆两本,一堆3本;(2)甲得一本,乙得两本,丙得三本;
(3)一人得一本,一人得两本,一人得三本;(4)平均分给甲、乙、丙三人;(5)平均分成三堆。
查看答案和解析>>
科目:高中数学 来源:2014届江苏省高二下学期期中考试数学理科试卷(解析版) 题型:解答题
有6本不同的书,按照以下要求处理,各有多少种不同的分法?
(1)一堆一本,一堆两本,一堆三本;
(2)甲得一本,乙得两本,丙得三本;
(3)一人得一本,一人得二本,一人得三本;
(4)平均分给甲、乙、丙三人;
(5)平均分成三堆.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com