
【题目】设函数![]() ,
,![]() ,其中
,其中![]() .
.
(1)若![]() 是关于
是关于![]() 的不等式
的不等式![]() 的解,求
的解,求![]() 的取值范围;
的取值范围;
(2)求函数![]() 在
在![]() 上的最小值;
上的最小值;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(4)当![]() 时,令
时,令![]() ,试研究函数
,试研究函数![]() 的单调性,求
的单调性,求![]() 在该区间上的最小值.
在该区间上的最小值.
【答案】(1)![]() ;(2)
;(2)  ;(3)
;(3)![]() ;(4)在
;(4)在![]() 单调递减,在
单调递减,在![]() 单调递增;最小值为
单调递增;最小值为![]() ,
,
【解析】
(1)在不等式![]() 中令
中令![]() ,则可以得到关于
,则可以得到关于![]() 的不等式,其解即为
的不等式,其解即为![]() 的取值范围.
的取值范围.
(2)就是![]() 、
、![]() 分类讨论函数的单调性后可求
分类讨论函数的单调性后可求![]() 在
在![]() 上的最小值.
上的最小值.
(3)由![]() 可得实数
可得实数![]() 的取值范围.
的取值范围.
(4)设任意![]() ,考虑
,考虑![]() 的符号后可得
的符号后可得![]() 的单调性,从而可求
的单调性,从而可求![]() 的最小值.
的最小值.
(1)由题设有![]() ,故
,故![]() ,故
,故![]() .
.
(2)若![]() ,
,
设任意的![]() ,则
,则![]() ,
,
因为![]() ,故
,故![]() ,
,![]() ,
,
所以![]() 即
即![]() ,所以
,所以![]() 为
为![]() 上的减函数,
上的减函数,
故![]() 的最小值为
的最小值为![]() .
.
若![]() ,则
,则
设任意的![]() ,则
,则![]() ,
,
因为![]() ,故
,故![]() ,
,![]() ,
,
所以![]() 即
即![]() ,所以
,所以![]() 为
为![]() 上的减函数,
上的减函数,
同理可证:![]() 为
为![]() 上的增函数.
上的增函数.
所以![]() 的最小值为
的最小值为![]() ,
,
故 .
.
(3)因为对任意的![]() ,不等式
,不等式![]() 恒成立,
恒成立,
故![]() .
.
由(2)可知:当![]() 时,由
时,由![]() ,当
,当![]() 时,由
时,由![]() ,
,
所以 或
或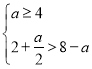 即
即![]() (无解)或
(无解)或![]() ,
,
故![]() .
.
(4)若![]() ,则
,则![]() ,
,
设任意的![]() ,则
,则 ,
,
因为![]() ,故
,故![]() ,
,![]() ,
,
所以![]() 即
即![]() ,所以
,所以![]() 为
为![]() 上的减函数,
上的减函数,
同理可证![]() 为
为![]() 上的增函数,
上的增函数,
所以![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知![]() (cosx,2cosx),
(cosx,2cosx),![]() (2cosx,sinx),f(x)
(2cosx,sinx),f(x)![]()
![]() .
.
(1)把f(x)的图象向右平移![]() 个单位得g(x)的图象,求g(x)的单调递增区间;
个单位得g(x)的图象,求g(x)的单调递增区间;
(2)当![]() 与
与![]() 共线时,求f(x)的值.
共线时,求f(x)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018衡水金卷(三)】如图所示,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(I)证明: ![]() 平面
平面![]() ;
;
(II)若二面角![]() 的平面角的大小为
的平面角的大小为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
函数![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() 。
。
(1)求实数a,b,并确定函数![]() 的解析式;
的解析式;
(2)判断![]() 在(-1,1)上的单调性,并用定义证明你的结论;
在(-1,1)上的单调性,并用定义证明你的结论;
(3)写出![]() 的单调减区间,并判断
的单调减区间,并判断![]() 有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
A. 甲地:总体均值为3,中位数为4 B. 乙地:总体均值为1,总体方差大于0
C. 丙地:中位数为2,众数为3 D. 丁地:总体均值为2,总体方差为3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某民营企业生产![]() 两种产品,根据市场调查与预测,
两种产品,根据市场调查与预测,![]() 产品的利润与投资成正比,其关系如图甲,
产品的利润与投资成正比,其关系如图甲,![]() 产品的利润与投资的算术平方根成正比,其关系如图乙(注:利润与投资单位:万元).
产品的利润与投资的算术平方根成正比,其关系如图乙(注:利润与投资单位:万元).

(1)分别将![]() 两种产品的利润表示为投资
两种产品的利润表示为投资![]() (万元)的函数关系式;
(万元)的函数关系式;
(2)该企业已筹集到10万元资金,并全部投入![]() 两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元?
两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点.用![]() ,
,![]() 分别表示乌龟和兔子所行的路程,
分别表示乌龟和兔子所行的路程,![]() 为时间,则与故事情节相吻合的是( )
为时间,则与故事情节相吻合的是( )
A.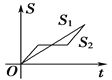 B.
B.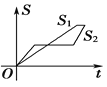 C.
C.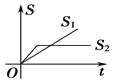 D.
D.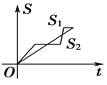
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元.设该公司的仪器月产量为![]() 台,当月产量不超过400台时,总收益为
台,当月产量不超过400台时,总收益为![]() 元,当月产量超过400台时,总收益为
元,当月产量超过400台时,总收益为![]() 元.(注:总收益=总成本+利润)
元.(注:总收益=总成本+利润)
(1)将利润表示为月产量![]() 的函数
的函数![]() ;
;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com